��Ŀ����
��ͼ�٣���ƽ��ֱ������ϵ�У�A(a��0)��C(b��2)��������(a��2)2��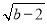 ��0����C��CB��x����B.
��0����C��CB��x����B.
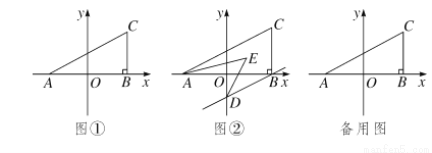
(1)��������ABC�������
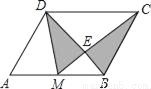
(2)��ͼ�ڣ�����B��BD��AC��y����D����AE��DE�ֱ�ƽ�֡�CAB����ODB�����AED�Ķ�����
(3)��y�����Ƿ���ڵ�P��ʹ��������ACP��������ABC�������ȣ������ڣ����P������ꣻ�������ڣ���˵�����ɣ�
(1)4;(2) 45��;(3) P�������Ϊ(0����1)��(0��3)�� �������������������1�����ݷǸ��������ʵ�a+2=0��b-2=0�����a=-2��b=2����A��-2��0����C��2��2����B��2��0����Ȼ����������������ʽ����S��ABC�� ��2����EM��AC����ͼ�ڣ���AC��EM��BD������ƽ���ߵ����ʵá�CAE=��AEM����BDE=��DEM�����AED=��CAE+��BDE����...
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ


 B.
B.  C.
C.  D.
D. 
 B.
B.  C.
C.  D.
D. 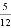
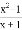 ����������ȵ�ʵ��
����������ȵ�ʵ��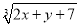 ��3����x2��y2��ƽ������
��3����x2��y2��ƽ������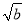 ��a.����4*9��
��a.����4*9��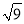 ��4��7����ô15*196��________��
��4��7����ô15*196��________��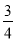 +
+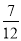 ��
��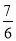 ��������60����
��������60����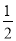 ����3��|3������3��2|��
����3��|3������3��2|��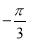 ��0����0.333����
��0����0.333����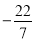 ��
�� 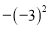 ��2.010010001������������������
��2.010010001������������������