题目内容
如图,点A、B、C分别是⊙O上的点,∠ B=60°, CD是⊙ O的直径,P是CD延长线上的点,且AP=AC.
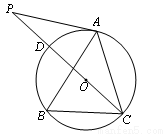
(1)求证:AP是⊙O的切线;
(2)若AC= 3,求PD的长
(1)证明见解析;(2)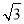
【解析】
试题分析:(1)连接OA,求出∠AOC,求出∠ACP,得出∠P,求出∠AOD,推出∠PAO=90°,根据切线判定推出即可;
(2)根据∠ACD=30°,AC=3求出DC,求出半径,在Rt△PAO中根据勾股定理求出即可.
试题解析:(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
∵OA=OC,
∴∠ACP=∠CAO=30°,
∴∠AOP=60°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=90°,
即OA⊥AP,
∵点A在⊙O上,
∴AP是⊙O的切线.
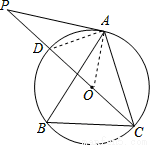
(2)【解析】
连接AD,
∵CD是⊙O的直径,
∴∠CAD=90°,
∴AD=AC?tan30°=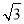 ,CD=2AD=2
,CD=2AD=2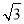 ,
,
∴DO=AO=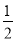 CD=
CD=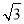 ,
,
在Rt△PAO中,由勾股定理得:PA2+AO2=PO2,
∴32+(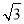 )2=(PD+
)2=(PD+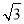 )2,
)2,
∵PD的值为正数,
∴PD=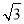 .
.
考点:切线的判定.

练习册系列答案
相关题目

 B.
B.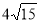 C.8 D.10
C.8 D.10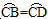 ,CF⊥AB于点F,CE⊥AD的延长线于点E.
,CF⊥AB于点F,CE⊥AD的延长线于点E.



 有意义的x的取值范围是 .
有意义的x的取值范围是 .