题目内容
某小区在绿化工程中有一块长为20m、宽为8m的矩形空地，计划在其中修建两块相同的矩形绿地，使它们的面积之和为56m2，两块绿地之间及周边留有宽度相等的人行通道（如图所示），求人行通道的宽度．考点：一元二次方程的应用
专题：几何图形问题
分析：根据矩形的面积和为56平方米列出一元二次方程求解即可．
解答：解：设人行道的宽度为x米，根据题意得，
（20-3x）（8-2x）=56，
解得：x1=2，x2=
（不合题意，舍去）．
答：人行道的宽为2米．
（20-3x）（8-2x）=56，
解得：x1=2，x2=
| 26 |
| 3 |
答：人行道的宽为2米．
点评：本题考查了一元二次方程的应用，利用两块矩形的面积之和为56m2得出等式是解题关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
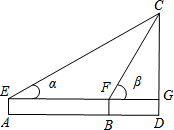小红想要测量校园内一座教学楼CD的高度．她先在A处测得楼顶C的仰角α=30°，再向楼的方向直行10米到达B处，又测得楼顶C的仰角β=60°，若小红的目高（眼睛到地面的高度）AE为1.60米，请你帮助她计算出这座教学楼CD的高度（结果精确到0.1米）参考数据：
为了维护海洋权益，新组建的国家海洋局加强了海洋巡逻力度，如图，一艘海监船位于灯塔P的南向东45°方向，距离灯塔200海里的A处，沿正北方向航行一段时间后，到达位于灯塔P的北偏东30°方向上的B处．
如图，在△ABC中，BD平分∠ABC，∠ACE是△ABC的外角，CD平分∠ACE，∠A=50°，则∠D的度数为
如图，已知AB是⊙O的直径，点C在⊙O上，若∠CAB=35°，求∠ABC的度数．等腰三角形一腰上的高与另一腰的夹角为60°，则顶角的度数为（ ）
| A、30° |
| B、60° |
| C、60°或120° |
| D、30°或150° |
在平面直角坐标系中，已知点E（-4，2），F（-2，-2），以原点O为位似中心，相似比为
，把△EFO缩小，则点E的对应点E′的坐标是（ ）
| 1 |
| 2 |
| A、（-2，1） |
| B、（-8，4） |
| C、（-2，1）或（2，-1） |
| D、（-8，4）或（8，-4） |
当x=1时，代数式x2+2x+1的值是（ ）
| A、-2 | B、-1 | C、0 | D、4 |