题目内容
 如图所示,抛物线y=-(x-1)2+4与x轴交于A、B两点,与y轴交于C点,顶点为D.若抛物线上有一点P(点P不与点C重合),使得S△DCB=S△PCB,则这样的点P总共存在
如图所示,抛物线y=-(x-1)2+4与x轴交于A、B两点,与y轴交于C点,顶点为D.若抛物线上有一点P(点P不与点C重合),使得S△DCB=S△PCB,则这样的点P总共存在考点:抛物线与x轴的交点
专题:
分析:由S△DCB=S△PCB为突破口,将直线BC沿y轴上下移动,得到该直线与抛物线y=-(x-1)2+4的三个交点,这三个交点即为所求的点P.
解答: 解:∵S△DCB=S△PCB,
解:∵S△DCB=S△PCB,
∴△DCB与△PCB是同底等高的两个三角形,
∴点P所在的直线与直线BC平行,且点P、D到直线BC的距离相等,
如图,满足条件的点P有3个.
故答案是:3.
 解:∵S△DCB=S△PCB,
解:∵S△DCB=S△PCB,∴△DCB与△PCB是同底等高的两个三角形,
∴点P所在的直线与直线BC平行,且点P、D到直线BC的距离相等,
如图,满足条件的点P有3个.
故答案是:3.
点评:本题考查了抛物线与x轴的交点.解题时利用了“数形结合”的数学思想,减少了繁琐的数学计算过程.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 如图,数轴上A点表示的数可能是( )
如图,数轴上A点表示的数可能是( )A、
| ||
B、
| ||
C、
| ||
D、
|
在
,sin45°,
-1,
,(
)0,-
,(
)-2,1.732,
中任取一个,是无理数的概率是( )
| 25 |
| 3 |
| 3 |
| π |
| 3 |
| 5 |
| 16 |
| 3 |
| 3 | 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列各数中,最大的数是( )
A、
| ||
| B、0 | ||
| C、|-4| | ||
| D、π |
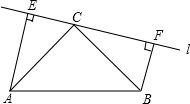 如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足为E,F.
如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足为E,F.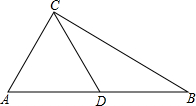 在Rt△ABC中,∠C=90°,BC=2
在Rt△ABC中,∠C=90°,BC=2 如图,AD⊥BC于点D,DE⊥AC于点E,DF⊥AB于点F,则表示A点到BC,D点到AB、AC的距离是
如图,AD⊥BC于点D,DE⊥AC于点E,DF⊥AB于点F,则表示A点到BC,D点到AB、AC的距离是 已知,△ABC三个顶点的坐标分别为A(-3,0),B(-3,-4),C(-1,-4).
已知,△ABC三个顶点的坐标分别为A(-3,0),B(-3,-4),C(-1,-4).