题目内容
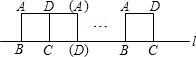 将边长为4cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是
将边长为4cm的正方形ABCD的四边沿直线l向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是考点:弧长的计算,旋转的性质
专题:
分析:可先计算旋转周时,正方形的顶点A所经过的路线的长,可以看出是四段弧长,根据弧长公式计算即可.
解答:解:第一次旋转是以点C为圆心,AC为半径,旋转角度是90度,
所以弧长=
=2
π;
第二次旋转是以点D为圆心,AD为半径,角度是90度,
所以弧长=
=2π;
第三次旋转是以点A为圆心,所以没有路程;
第四次是以点B为圆心,AB为半径,角度是90度,
所以弧长=2π;
所以旋转一周的弧长共=2
π+4π.
所以正方形滚动两周正方形的顶点A所经过的路线的长是4
π+8π.
故答案为:4
π+8π.
所以弧长=
90π×4
| ||
| 180 |
| 2 |
第二次旋转是以点D为圆心,AD为半径,角度是90度,
所以弧长=
| 90π×4 |
| 180 |
第三次旋转是以点A为圆心,所以没有路程;
第四次是以点B为圆心,AB为半径,角度是90度,
所以弧长=2π;
所以旋转一周的弧长共=2
| 2 |
所以正方形滚动两周正方形的顶点A所经过的路线的长是4
| 2 |
故答案为:4
| 2 |
点评:本题考查了弧长公式的计算,关键是理清第一次旋转时的圆心及半径和圆心角的度数,然后利用弧长公式求解.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图,数轴上A点表示的数可能是( )
如图,数轴上A点表示的数可能是( )A、
| ||
B、
| ||
C、
| ||
D、
|
在
,sin45°,
-1,
,(
)0,-
,(
)-2,1.732,
中任取一个,是无理数的概率是( )
| 25 |
| 3 |
| 3 |
| π |
| 3 |
| 5 |
| 16 |
| 3 |
| 3 | 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
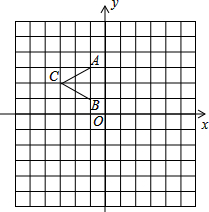 如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)
如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2) 如图,AB是⊙O的直径,弦CD⊥AB,交AB于点E,∠CDB=30°,⊙O的半径为2cm,求弦CD的长.
如图,AB是⊙O的直径,弦CD⊥AB,交AB于点E,∠CDB=30°,⊙O的半径为2cm,求弦CD的长. 在Rt△ABC中,∠C=90°,BC=2
在Rt△ABC中,∠C=90°,BC=2