题目内容
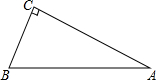 在△ABC中,∠ACB=90°,AC=4,BC=2,以AB为边向外作等腰直角三角形ABD,求CD的长.
在△ABC中,∠ACB=90°,AC=4,BC=2,以AB为边向外作等腰直角三角形ABD,求CD的长.考点:勾股定理,全等三角形的判定与性质,等腰直角三角形
专题:
分析:先分类讨论:(1)AB=BD,(2)AB=AD,(3)AD=BD,分别计算CD的值,即可解题.
解答: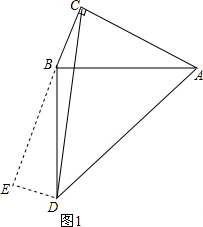 解:(1)如图1所示,当AB=BD时,作DE⊥BE,
解:(1)如图1所示,当AB=BD时,作DE⊥BE,
∵∠CAB+∠ABC=90°,∠ABC+∠DBE=90°,
∴∠CAB=∠DBE,
在△BED和△ACB中,
,
∴△BED≌△ACB(AAS),
∴BE=AC=4,DE=BC=2,
∴CD=
=2
;
(2)如图2所示,当AB=AD时,作DE⊥AE,
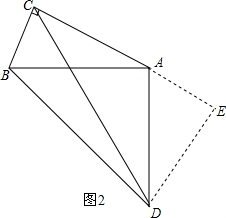 ∵∠CAB+∠ABC=90°,∠BAC+∠DAE=90°,
∵∠CAB+∠ABC=90°,∠BAC+∠DAE=90°,
∴∠ABC=∠DAE,
在△DEA和△ACB中,
,
∴△DEA≌△ACB(AAS),
∴DE=AC=4,AE=BC=2,
∴CD=
=2
;
(3)如图3所示,当AD=BD时,作DE⊥AC,DF⊥CB延长线于F,
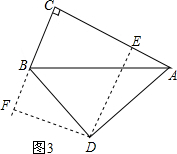 ∵∠ADE+∠BDE=90°,∠BDF+∠BDE=90°,
∵∠ADE+∠BDE=90°,∠BDF+∠BDE=90°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,
,
∴△ADE≌△BDF(AAS),
∴AE=BF,
∴AC+BC=AE+CE+CF-BF=2CE.
∴CE=3,
∴CD=3
.
综上所述,CD的长是2
或3
或2
;
 解:(1)如图1所示,当AB=BD时,作DE⊥BE,
解:(1)如图1所示,当AB=BD时,作DE⊥BE,∵∠CAB+∠ABC=90°,∠ABC+∠DBE=90°,
∴∠CAB=∠DBE,
在△BED和△ACB中,
|
∴△BED≌△ACB(AAS),
∴BE=AC=4,DE=BC=2,
∴CD=
| 62+22 |
| 10 |
(2)如图2所示,当AB=AD时,作DE⊥AE,
 ∵∠CAB+∠ABC=90°,∠BAC+∠DAE=90°,
∵∠CAB+∠ABC=90°,∠BAC+∠DAE=90°,∴∠ABC=∠DAE,
在△DEA和△ACB中,
|
∴△DEA≌△ACB(AAS),
∴DE=AC=4,AE=BC=2,
∴CD=
| 62+42 |
| 13 |
(3)如图3所示,当AD=BD时,作DE⊥AC,DF⊥CB延长线于F,
 ∵∠ADE+∠BDE=90°,∠BDF+∠BDE=90°,
∵∠ADE+∠BDE=90°,∠BDF+∠BDE=90°,∴∠ADE=∠BDF,
在△ADE和△BDF中,
|
∴△ADE≌△BDF(AAS),
∴AE=BF,
∴AC+BC=AE+CE+CF-BF=2CE.
∴CE=3,
∴CD=3
| 2 |
综上所述,CD的长是2
| 10 |
| 2 |
| 3 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
 已知,△ABC三个顶点的坐标分别为A(-3,0),B(-3,-4),C(-1,-4).
已知,△ABC三个顶点的坐标分别为A(-3,0),B(-3,-4),C(-1,-4).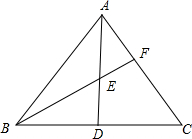 如图,AD是△ABC的中线,E为AD的中点,BE交AC于点F,AF=
如图,AD是△ABC的中线,E为AD的中点,BE交AC于点F,AF=