题目内容
 如图,从原点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆;…,按此规律,继续画半圆,则第6个半圆的面积为
如图,从原点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆;…,按此规律,继续画半圆,则第6个半圆的面积为考点:规律型:图形的变化类
专题:
分析:根据已知图形得出第5个半圆的半径,进而得出第5个半圆的面积,得出第n个半圆的半径,进而得出答案.
解答:解:∵以AB=1为直径画半圆,记为第1个半圆;
以BC=2为直径画半圆,记为第2个半圆;
以CD=4为直径画半圆,记为第3个半圆;
以DE=8为直径画半圆,记为第4个半圆,
∴第5个半圆的直径为16,
根据已知可得出第n个半圆的直径为:2n-1,
则第n个半圆的半径为:
=2n-2,
第n个半圆的面积为:
=22n-5π.
所以第6个半圆的面积为:128π.
故答案为:128π.
以BC=2为直径画半圆,记为第2个半圆;
以CD=4为直径画半圆,记为第3个半圆;
以DE=8为直径画半圆,记为第4个半圆,
∴第5个半圆的直径为16,
根据已知可得出第n个半圆的直径为:2n-1,
则第n个半圆的半径为:
| 2n-1 |
| 2 |
第n个半圆的面积为:
| π×(2n-2)2 |
| 2 |
所以第6个半圆的面积为:128π.
故答案为:128π.
点评:此题主要考查了图形的变化规律,注意数字之间变化规律,根据已知得出第n个半圆的直径为:2n-1是解题关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
已知⊙O1的半径为2cm,⊙O2的半径为3cm,且O1O2=1cm,则⊙O1和⊙O2的位置关系为( )
| A、内切 | B、相交 | C、外切 | D、外离 |
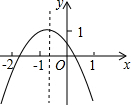 二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2-4ac.则M,N,P,Q中,值小于0的数有
二次函数y=ax2+bx+c(a≠0)的图象如图,若M=a+b-c,N=4a-2b+c,P=2a-b,Q=b2-4ac.则M,N,P,Q中,值小于0的数有 如图,在正方形网格中,tanC=
如图,在正方形网格中,tanC=