题目内容
如图，已知∠1=∠2，∠B=∠C，试证明AB∥CD．考点：平行线的判定与性质
专题：
分析：首先证明CE∥BF，得到∠C=∠3，从而证得∠3=∠B，根据内错角相等，两直线平行即可证得．
解答：解：∵∠1=∠2（已知），且∠1=∠4（对顶角相等），
∴∠2=∠4 （等量代换），
∴CE∥BF （同位角相等，两直线平行），
∴∠C=∠3（两直线平行，同位角相等）；
又∵∠B=∠C（已知），
∴∠3=∠B（等量代换），
∴AB∥CD （内错角相等，两直线平行）．
∴∠2=∠4 （等量代换），
∴CE∥BF （同位角相等，两直线平行），
∴∠C=∠3（两直线平行，同位角相等）；
又∵∠B=∠C（已知），
∴∠3=∠B（等量代换），
∴AB∥CD （内错角相等，两直线平行）．
点评：解答此题的关键是注意平行线的性质和判定定理的综合运用．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
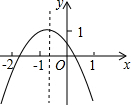二次函数y=ax2+bx+c（a≠0）的图象如图，若M=a+b-c，N=4a-2b+c，P=2a-b，Q=b2-4ac．则M，N，P，Q中，值小于0的数有已知⊙O1的半径为2cm，⊙O2的半径为3cm，且O1O2=1cm，则⊙O1和⊙O2的位置关系为（ ）
| A、内切 | B、相交 | C、外切 | D、外离 |
已知三个一次函数y=x+1，y=1-x和y=k（x-1）（k≠±1）的图象分别为直线l1，直线l2和直线l3，且l1、l2、l3两两相交．