题目内容
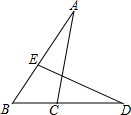 如图,△ABC≌△DBE,AB与DB,AC与DE是对应边,已知:∠B=43°,∠A=30°,求∠BED的度数.请你完善下面的推理步骤:解:∵∠A+∠B+∠BCA=180°(
如图,△ABC≌△DBE,AB与DB,AC与DE是对应边,已知:∠B=43°,∠A=30°,求∠BED的度数.请你完善下面的推理步骤:解:∵∠A+∠B+∠BCA=180°(∴∠BCA=
∵△ABC≌△DBE,(
∴∠BED=∠BCA=
考点:全等三角形的性质
专题:推理填空题
分析:根据三角形内角和定理求出∠BCA,根据全等三角形的性质得出∠BED=∠BCA,代入即可.
解答:解:∵∠A+∠B+∠BCA=180°(三角形内角和定理),∠B=43°,∠A=30°(已知),
∴∠BCA=107°,
∵△ABC≌△DBE(已知),
∴∠BED=∠BCA=107°(全等三角形的对应角相等),
故答案为:三角形内角和定理,已知,107°,已知,107°,
∴∠BCA=107°,
∵△ABC≌△DBE(已知),
∴∠BED=∠BCA=107°(全等三角形的对应角相等),
故答案为:三角形内角和定理,已知,107°,已知,107°,
点评:本题考查了全等三角形的性质和三角形的内角和定理的应用,注意:全等三角形的对应角相等,对应边相等,难度适中.

练习册系列答案
相关题目
计算-3x2(-2x+1)的结果是( )
| A、6x3+1 |
| B、6x3-3 |
| C、6x3-3x2 |
| D、6x3+3x2 |
 如图,在三角形ABC中,AB,AC的垂直平分线交BC于点E.G,若∠B+∠C=40°,则∠EAG=
如图,在三角形ABC中,AB,AC的垂直平分线交BC于点E.G,若∠B+∠C=40°,则∠EAG=