题目内容
在△ABC中,∠A=60°,AB=AC,BD平分∠ABC,DE⊥AB于点E,若CD=4,求AE的长.
考点:等边三角形的判定与性质
专题:
分析:由条件可判定△ABC为等边三角形,且D为AC中点,可知AD=CD=4,在Rt△ADE中,AE=
AD,求得结果.
| 1 |
| 2 |
解答: 解:∵∠A=60°,AB=AC,
解:∵∠A=60°,AB=AC,
∴△ABC为等边三角形,
∵BD平分∠ABC,
∴D为AC中点,且CD=4,
∴AD=CD=4,
∵DE⊥AB,且∠A=60°,
∴∠ADE=30°,
∴AE=
AD=2.
 解:∵∠A=60°,AB=AC,
解:∵∠A=60°,AB=AC,∴△ABC为等边三角形,
∵BD平分∠ABC,
∴D为AC中点,且CD=4,
∴AD=CD=4,
∵DE⊥AB,且∠A=60°,
∴∠ADE=30°,
∴AE=
| 1 |
| 2 |
点评:本题主要考查等边三角形的判定和性质及直角三角形的性质,由条件判定△ABC为等边三角形求得AD的长是解题的关键.

练习册系列答案
相关题目

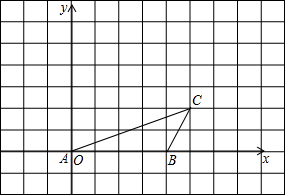 如图,已知点A、B、C的坐标分别为(0,0),(4,0),(5,2).将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.
如图,已知点A、B、C的坐标分别为(0,0),(4,0),(5,2).将△ABC绕点A按逆时针方向旋转90°得到△AB′C′. 如图,在方格纸中,△ABC的三个顶点和点P都在小方格的顶点上.将△ABC绕点P顺时针旋转180°,在图上画出旋转后的△A1B1C1.
如图,在方格纸中,△ABC的三个顶点和点P都在小方格的顶点上.将△ABC绕点P顺时针旋转180°,在图上画出旋转后的△A1B1C1.