题目内容
4．
如图，根据图形填空（1）∵∠A=∠4（已知）∴AC∥DE（同位角相等，两直线平行）
（2）∵∠2=∠4（已知）∴DF∥AB（内错角相等，两直线平行）
（3）∵∠2+∠6=180°（已知）∴AB∥DF（同旁内角互补，两直线平行）
（4）∵AB∥DF（已知）∴∠A+∠7=180°（两直线平行，同旁内角互补）．
分析 （1）根据同位角相等，两直线平行进行判断；
（2）根据内错角相等，两直线平行进行判断；
（3）根据同旁内角互补，两直线平行进行判断；
（4）根据两直线平行，同旁内角互补进行判断．
解答 解：（1）∵∠A=∠4（已知）
∴AC∥DE（同位角相等，两直线平行）
（2）∵∠2=∠4（已知）
∴DF∥AB（内错角相等，两直线平行）
（3）∵∠2+∠6=180°（已知）
∴AB∥DF（同旁内角互补，两直线平行）
（4）∵AB∥DF（已知）
∴∠A+∠7=180°（两直线平行，同旁内角互补）．
故答案为：（1）∠4；同位角相等，两直线平行；（2）∠4；内错角相等，两直线平行；（3）AB，DF，同旁内角互补，两直线平行；（4）7；两直线平行，同旁内角互补．
点评 本题主要考查了平行线的性质与判定的综合应用，解题时注意：平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
16．
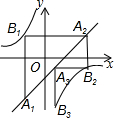如图，已知：n为正整数，点A1（x1，y1），A2（x2，y2），A3（x3，y3），A4（x4，y4）…An（xn，yn）均在直线y=x-1上，点B1（m1，p1），B2（m2，p2），B3（m3，p3）…Bn（mn，pn）均在双曲线y=-$\frac{1}{x}$上，并且满足：A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，A3B3⊥x轴，…，AnBn⊥x轴，BnAn+1⊥y轴，若点A1的横坐标为-1，则点A2017的坐标为（ ）
如图，已知：n为正整数，点A1（x1，y1），A2（x2，y2），A3（x3，y3），A4（x4，y4）…An（xn，yn）均在直线y=x-1上，点B1（m1，p1），B2（m2，p2），B3（m3，p3）…Bn（mn，pn）均在双曲线y=-$\frac{1}{x}$上，并且满足：A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，A3B3⊥x轴，…，AnBn⊥x轴，BnAn+1⊥y轴，若点A1的横坐标为-1，则点A2017的坐标为（ ）| A． | （-1，-2） | B． | （2，1） | C． | （$\frac{1}{2}$，$-\frac{1}{2}$） | D． | （$\frac{1}{2}$，-2） |
已知：有理数a、b、c在数轴上如图所示．化简：|a|+3|c-a|+|b+c|．
16．若式子$\sqrt{3-x}$有意义，在实数范围内有意义，则x的取值范围是（ ）
| A． | x≥3 | B． | x≤3 | C． | x＞3 | D． | x＜3 |