题目内容
11.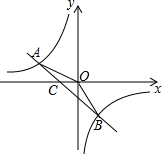 如图,已知点A(-2,1),B(1,n)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB交x轴于点C.
如图,已知点A(-2,1),B(1,n)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB交x轴于点C.(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
分析 (1)把点A坐标代入反比例函数的解析式得出m的值,再把点B坐标代入反比例函数的解析式得出n的值,把点A,B坐标代入一次函数的解析式得出k与b的值即可;
(2)令一次函数的y的值为0,得出点C坐标,把△AOB的面积分成△AOC的面积+△COB的面积.
解答 解:(1)∵点A(-2,1)在函数y=$\frac{m}{x}$的图象上,
∴m=-2,
∴反比例函数的解析式为y=-$\frac{2}{x}$,
∵点B(1,n)在函数y=-$\frac{2}{x}$的图象上,
∴n=-2,即B(1,-2),
∵y=kx+b经过A(-2,1)、B(1,-2),
∴$\left\{\begin{array}{l}{-2k+b=1}\\{k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
∴一次函数的解析式为y=-x-1;
(2)∵C是直线AB与x轴的交点,
∴当y=0时,x=-1,
∴点C(-1,0),即OC=1,
则S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×2=$\frac{3}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题,涉及的知识有:坐标与图形性质,直线与坐标轴的交点,待定系数法求函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.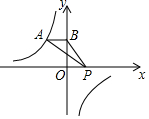 如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
 如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )
如图,A为反比例函数y=$\frac{k}{x}$图象上的一点,AB⊥y轴于B,点P在x轴上,S△ABP=2,则这个反比例函数的表达式为( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
3.下列语句中,说法错误的是( )
| A. | 点(0,0)是坐标原点 | |
| B. | 对于坐标平面内的任一点,都有唯一的一对有序实数与它对应 | |
| C. | 点A(a,-b )在第二象限,则点B(-a,b)在第四象限 | |
| D. | 若点P的坐标为(a,b),且a•b=0,则点P一定在坐标原点 |
20.若a,b是实数,且a2=$\sqrt{b-1}+\sqrt{1-b}+4$,则a+b的值是( )
| A. | 3或-3 | B. | 3或-1 | C. | -3或-1 | D. | 3或1 |
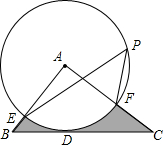 如图,△ABC中,BC=8cm,以A为圆心,以2cm为半径的圆与BC相切于点D,交AB于点E,交AC于点F,点P在圆上,∠EPF=50°,则图中阴影部分的面积为8-$\frac{10}{9}$πcm2.
如图,△ABC中,BC=8cm,以A为圆心,以2cm为半径的圆与BC相切于点D,交AB于点E,交AC于点F,点P在圆上,∠EPF=50°,则图中阴影部分的面积为8-$\frac{10}{9}$πcm2.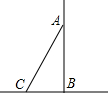 如图,将长为6米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底端B的距离AB.
如图,将长为6米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底端B的距离AB. 如图,∠1=118°,∠2=62°,则a与b的位置关系是a∥b.
如图,∠1=118°,∠2=62°,则a与b的位置关系是a∥b.