题目内容
1.一只不透明的袋子里共有4个球,其中3个白球,1个红球,它们除颜色外均相同:(1)从袋子中随机摸出一个球是白球的概率是$\frac{3}{4}$;
(2)从袋子中随机摸出一个球,不放回袋子,摇匀袋子后再摸一个球,请用列表或画树状图的方法,求出两次摸出的球一个是白球,一个是红球的概率.
分析 (1)根据总球的个数和概率公式进行计算即可;
(2)根据题意先画出树状图,然后根据概率公式列式计算即可得解.
解答 解:(1)∵共有4个球,其中3个白球,1个红球,
∴P(摸出一个球是白球)=$\frac{3}{4}$;
故答案为:$\frac{3}{4}$;
(2)根据题意画树形图如下:
共有12中等可能的结果,P(两次摸出的求都是白球)=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.

练习册系列答案
相关题目
11.化简$\frac{1}{x-1}$+$\frac{2}{1-{x}^{2}}$结果是( )
| A. | x-1 | B. | x+1 | C. | $\frac{x+3}{{x}^{2}-1}$ | D. | $\frac{1}{x+1}$ |
9.已知等腰三角形的一个内角是70°,则这个等腰三角形的顶角为( )
| A. | 70° | B. | 40° | C. | 70°或40° | D. | 以上答案都不对 |
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有公共点,则r的取值范围是1≤r≤$\sqrt{10}$.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有公共点,则r的取值范围是1≤r≤$\sqrt{10}$. 如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动2,6,8秒时,△DEB与△BCA全等.
如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动2,6,8秒时,△DEB与△BCA全等.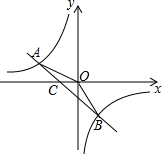 如图,已知点A(-2,1),B(1,n)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB交x轴于点C.
如图,已知点A(-2,1),B(1,n)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB交x轴于点C.