题目内容
6. 如图,CD是⊙O的直径,点E在⊙O上,A为DC延长线上一点,连接AE交⊙O于点B,且⊙O得半径为2,若∠EOD=3∠A,求AB的长.
如图,CD是⊙O的直径,点E在⊙O上,A为DC延长线上一点,连接AE交⊙O于点B,且⊙O得半径为2,若∠EOD=3∠A,求AB的长.
分析 连接OB,根据三角形外角的性质可知∠EOD=∠A+∠AEO,再由∠EOD=3∠A可知∠AEO=2∠A,故可得出∠EBO=2∠A,所以∠AOB=∠A,进而可得出结论.
解答  解:连接OB,
解:连接OB,
∵∠EOD=∠A+∠AEO,∠EOD=3∠A,
∴∠AEO=2∠A.
∵OB=OE=2,
∴∠EBO=2∠A.
∵∠EBO=∠A+∠AOB,
∴∠AOB=∠A,
∴AB=OB=2.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
18. 点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
 点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )| A. | 1 cm | B. | 2 cm | C. | 4 cm | D. | 6 cm |
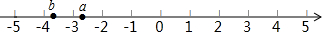 我们知道:a、b在数轴上对应的A、B两点之间距离|AB|=|a-b|
我们知道:a、b在数轴上对应的A、B两点之间距离|AB|=|a-b|
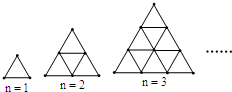 如图,是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边摆上20(n=20)根时,需火柴棍为630 根,若当每边摆上n根时,试写出需火柴棍为$\frac{3n(1+n)}{2}$ 根.
如图,是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边摆上20(n=20)根时,需火柴棍为630 根,若当每边摆上n根时,试写出需火柴棍为$\frac{3n(1+n)}{2}$ 根.