题目内容
8.观察下列等式:①$\sqrt{{5^2}-{4^2}}$=1×3;②$\sqrt{{{17}^2}-{8^2}}$=3×5;③$\sqrt{{{37}^2}-{{12}^2}}$=5×7;
…
根据上述规律解决下列问题:
(1)完成第④个等式:$\sqrt{{{65}^2}-{{16}^2}}$=7×9;
(2)写出你猜想的第n个等式(用含n的式子表示),并证明其正确性.
分析 根据规律化简即可.
解答 解:(1)∵①$\sqrt{{5^2}-{4^2}}$=$\sqrt{(5-4)×(5+4)}$=1×3;
②$\sqrt{{{17}^2}-{8^2}}$=$\sqrt{(17-8)×(17+8)}$=3×5;
③$\sqrt{{{37}^2}-{{12}^2}}$=$\sqrt{(37-12)×(37+12)}$=5×7;
…
∴$\sqrt{{65}^{2}-1{6}^{2}}$=$\sqrt{(65-16)×(65+16)}$=7×9;
故答案为:7,9;
(2)由(1)知,第n个等式$\sqrt{{{({4{n^2}+1})}^2}-16{n^2}}$=(2n-1)(2n+1),
证明如下:$\sqrt{{{({4{n^2}+1})}^2}-16{n^2}}=\sqrt{({4{n^2}-4n+1})({4{n^2}+4n+1})}=\sqrt{{{({2n-1})}^2}{{({2n+1})}^2}}=({2n-1})({2n+1})$.
点评 本题主要考查了二次根式的性质及化简,根据已知找出规律是解答此题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
16.某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长在(单位:cm)在5~50之间.每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)有基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的.浮动价与薄板的边长成正比例.在营销过程中得到了表格中的数据.已知出厂一张边长为40cm的薄板,获得的利润为26元.
(1)求一张薄板的出厂价与边长之间满足的函数关系式;
(2)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?
(3)若限定薄板的边长不超过20cm,浮动价下降a%,其他条件不变,薄板的利润随边长的增加而增大时,直接写出a的取值范围.
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
(2)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?
(3)若限定薄板的边长不超过20cm,浮动价下降a%,其他条件不变,薄板的利润随边长的增加而增大时,直接写出a的取值范围.
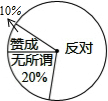 “校园手机”现象越来越受到社会的关注,“五一”期间,小记者刘涵随机调查了城区若干名家长对中学生带手机现象的看法,统计整理并制作了如图的统计图,家长“反对”的圆心角的度数是252°.
“校园手机”现象越来越受到社会的关注,“五一”期间,小记者刘涵随机调查了城区若干名家长对中学生带手机现象的看法,统计整理并制作了如图的统计图,家长“反对”的圆心角的度数是252°.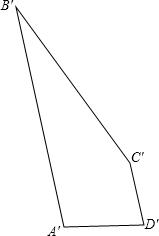 如图所示,四边形A′B′C′D′是将四边形ABCD平移后得到的,已知A′B′=13,B′C′=12,C′D′=3,D′A′=4,求四边形ABCD的周长.
如图所示,四边形A′B′C′D′是将四边形ABCD平移后得到的,已知A′B′=13,B′C′=12,C′D′=3,D′A′=4,求四边形ABCD的周长.
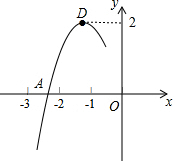 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论: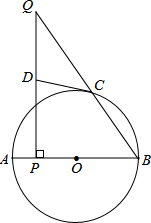 如图,AB是⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
如图,AB是⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.