题目内容
20.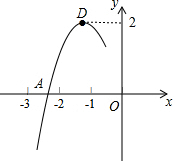 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;
②当x>-1时y随x增大而减小;
③a+b+c<0;
④若方程ax2+bx+c-m=0没有实数根,则m>2;
⑤3a+c<0.
其中,正确结论的序号是②③④⑤.
分析 ①根据抛物线与x轴有两个交点,可得b2-4ac>0,据此解答即可.
②根据抛物线的对称轴x=-1,可得当x>-1时,y随x增大而减小,据此判断即可.
③根据抛物线与x轴的一个交点A在点(-3,0)和(-2,0)之间,可得抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,所以当x=1时,y<0,据此判断即可.
④根据y=ax2+bx+c的最大值是2,可得方程ax2+bx+c-m=0没有实数根,则m>2,据此判断即可.
⑤首先根据抛物线的对称轴x=-$\frac{b}{2a}$=-1,可得b=2a,然后根据a+b+c<0,判断出3a+c<0即可.
解答 解:∵抛物线与x轴有两个交点,
∴b2-4ac>0,
∴结论①不正确.
∵抛物线的对称轴x=-1,
∴当x>-1时,y随x增大而减小,
∴结论②正确.
∵抛物线与x轴的一个交点A在点(-3,0)和(-2,0)之间,
∴抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,
∴当x=1时,y<0,
∴a+b+c<0,
∴结论③正确.
∵y=ax2+bx+c的最大值是2,
∴方程ax2+bx+c-m=0没有实数根,则m>2,
∴结论④正确.
∵抛物线的对称轴x=-$\frac{b}{2a}$=-1,
∴b=2a,
∵a+b+c<0,
∴a+2a+c<0,
∴3a+c<0,
∴结论⑤正确.
综上,可得
正确结论的序号是:②③④⑤.
故答案为:②③④⑤.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| A. | (-2015)-1 | B. | -(2015)-1 | C. | (-1)×(-2015) | D. | (-2015)÷2015 |
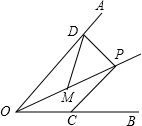 如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
| A. | 小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是$\frac{3}{10}$ | |
| B. | 随机抛掷一枚均匀的硬币,落地后反面一定朝上 | |
| C. | 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖 | |
| D. | 在一次课堂进行的抛硬币试验中,同学们估计硬币落地后正面朝上的概率为0.51 |
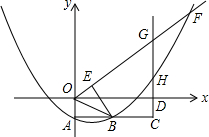 如图,抛物线y=$\frac{1}{2}$x2+mx-n(n>0)与y轴交于点A,过点A作AB∥x轴,交抛物线于点B,延长AB到C,使BC=AB,过点C作CD⊥x轴于点D(4n,0).
如图,抛物线y=$\frac{1}{2}$x2+mx-n(n>0)与y轴交于点A,过点A作AB∥x轴,交抛物线于点B,延长AB到C,使BC=AB,过点C作CD⊥x轴于点D(4n,0).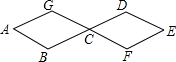 蜜蜂采蜜时,如果蜜源很远它就会跳起“8字舞”,告诉同伴蜜源的方向.如图所示,两个全等菱形的边长为1厘米,一只蜜蜂由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,飞行2015厘米后停下,则这只蜜蜂停在G点.
蜜蜂采蜜时,如果蜜源很远它就会跳起“8字舞”,告诉同伴蜜源的方向.如图所示,两个全等菱形的边长为1厘米,一只蜜蜂由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,飞行2015厘米后停下,则这只蜜蜂停在G点.