题目内容
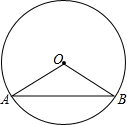 如图,弦AB把圆周分成1:2两部分,已知⊙O的半径为1,求弦AB的长.
如图,弦AB把圆周分成1:2两部分,已知⊙O的半径为1,求弦AB的长.考点:垂径定理,勾股定理,圆心角、弧、弦的关系
专题:
分析:过O作OC⊥AB于C,求出∠AOB的度数,根据等腰三角形的性质求出∠AOC的度数,解直角三角形求出AC,根据垂径定理得出AB=2AC求出即可.
解答:解:
过O作OC⊥AB于C,
∵弦AB把圆周分成1:2两部分,
∴∠AOB=
×360°=120°,
∵OA=OB,OC⊥AB,
∴∠AOC=60°,∠ACO=90°,
∵OA=1,
∴AC=1×sin60°=
,
∵OC⊥AB,OC过O,
∴AB=2AC=
.

过O作OC⊥AB于C,
∵弦AB把圆周分成1:2两部分,
∴∠AOB=
| 1 |
| 3 |
∵OA=OB,OC⊥AB,
∴∠AOC=60°,∠ACO=90°,
∵OA=1,
∴AC=1×sin60°=
| ||
| 2 |
∵OC⊥AB,OC过O,
∴AB=2AC=
| 3 |
点评:本题考查了垂径定理,解直角三角形的应用,解此题的关键是能构造直角三角形,题目是一道比较好的题目,难度适中.

练习册系列答案
相关题目
 如图,直线l上有甲、乙、丙三个正方形,若甲、丙的面积分别为5和11,则乙的面积为( )
如图,直线l上有甲、乙、丙三个正方形,若甲、丙的面积分别为5和11,则乙的面积为( )| A、4 | B、6 | C、16 | D、55 |
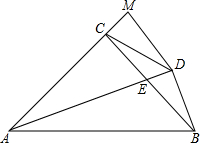 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,且CD=BD.下列结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,且CD=BD.下列结论:①AC+CE=AB;②CD=
| 1 |
| 2 |
其中正确的结论有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
A为数轴上表示-5的点,将A沿数轴向左移动2个单位长度到B点,则B点到原点的距离为( )
| A、3 | B、7 | C、-3 | D、-7 |
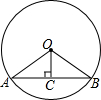 已知:如图,在半径为R的⊙O中,∠AOB=2α,OC⊥AB于C点.
已知:如图,在半径为R的⊙O中,∠AOB=2α,OC⊥AB于C点.  如图,在△ABC中,CD是∠C的角平分线,∠A=2∠B,求证:BC=AC+AD.
如图,在△ABC中,CD是∠C的角平分线,∠A=2∠B,求证:BC=AC+AD. 已知D,E分别为△ABC的边BC、AC中点,BE与AD交于点G,EF∥BC交AD于F,则AF:FG=
已知D,E分别为△ABC的边BC、AC中点,BE与AD交于点G,EF∥BC交AD于F,则AF:FG= 已知在△ABC中,AB=BC,AD=AC=BD,求∠DAC的度数.
已知在△ABC中,AB=BC,AD=AC=BD,求∠DAC的度数.