题目内容
 如图,直线l上有甲、乙、丙三个正方形,若甲、丙的面积分别为5和11,则乙的面积为( )
如图,直线l上有甲、乙、丙三个正方形,若甲、丙的面积分别为5和11,则乙的面积为( )| A、4 | B、6 | C、16 | D、55 |
考点:全等三角形的判定与性质,勾股定理,正方形的性质
专题:
分析:易证∠BCA=∠EAD,即可证明△ABC≌△EDA,可得AB=DE,根据勾股定理即可求得AC2的值,即可解题.
解答:解:如图,
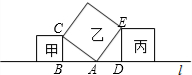
∵∠BAC+∠EAD=90°,∠BAC+∠BCA=90°,
∴∠BCA=∠EAD,
在△ABC和△EDA中,
,
∴△ABC≌△EDA(AAS),
∴AB=DE,
∵BC2=5,DE2=11,
∴AC2=AB2+BC2=DE2+BC2=11+5=16.
故选:C.

∵∠BAC+∠EAD=90°,∠BAC+∠BCA=90°,
∴∠BCA=∠EAD,
在△ABC和△EDA中,
|
∴△ABC≌△EDA(AAS),
∴AB=DE,
∵BC2=5,DE2=11,
∴AC2=AB2+BC2=DE2+BC2=11+5=16.
故选:C.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△ABC≌△EDA是解题的关键.

练习册系列答案
相关题目
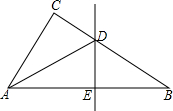 如图,△ABC中,∠C=90°,AB的中垂线DE交AB于E,交BC于D,若CB=8,AC=6,则△ACD的周长为( )
如图,△ABC中,∠C=90°,AB的中垂线DE交AB于E,交BC于D,若CB=8,AC=6,则△ACD的周长为( )| A、16 | B、14 | C、20 | D、18 |
下列各数与2的和是0的是( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
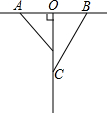 如图所示,AO=BO=50cm,OC是一条射线,OC⊥AB于点O,一只甲虫由点A以2cm/s的速度向B爬行,同时另一只甲虫由点O以3cm/s的速度沿OC方向爬行,是否存在这样的时刻,使两只甲虫与点O组成的三角形的面积为450cm2?若存在,请说明在什么时刻;若不存在,请说明理由.
如图所示,AO=BO=50cm,OC是一条射线,OC⊥AB于点O,一只甲虫由点A以2cm/s的速度向B爬行,同时另一只甲虫由点O以3cm/s的速度沿OC方向爬行,是否存在这样的时刻,使两只甲虫与点O组成的三角形的面积为450cm2?若存在,请说明在什么时刻;若不存在,请说明理由. 如图,⊙O与⊙O1内切于点A,⊙O的弦交⊙O1于点C,P是⊙O上一点,若∠AO1C=110°,求∠P的度数.
如图,⊙O与⊙O1内切于点A,⊙O的弦交⊙O1于点C,P是⊙O上一点,若∠AO1C=110°,求∠P的度数. 如图,在Rt△ABC中∠ABC=90°,BA=BC,P在△ABC的内部,且∠APB=135°,PA:PC=1:3,求PA:PB.
如图,在Rt△ABC中∠ABC=90°,BA=BC,P在△ABC的内部,且∠APB=135°,PA:PC=1:3,求PA:PB. 如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是
如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是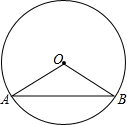 如图,弦AB把圆周分成1:2两部分,已知⊙O的半径为1,求弦AB的长.
如图,弦AB把圆周分成1:2两部分,已知⊙O的半径为1,求弦AB的长.