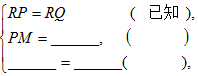题目内容
16. 如图,已知△ABC中,点F在边AB上,且AF=$\frac{2}{5}$AB、过A作AG∥BC交CF的延长线于点G.
如图,已知△ABC中,点F在边AB上,且AF=$\frac{2}{5}$AB、过A作AG∥BC交CF的延长线于点G.(1)设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$和$\overrightarrow{b}$表示向量$\overrightarrow{AG}$;
(2)在图中求作向量$\overrightarrow{AG}$与$\overrightarrow{AB}$的和向量.
(不要求写作法,但要指出所作图中表示结论的向量)
分析 (1)证△AGF∽△BCF得$\frac{AG}{BC}$=$\frac{AF}{BF}$=$\frac{2}{3}$,即AG=$\frac{2}{3}$CB,由$\overrightarrow{AG}=\frac{2}{3}$$\overrightarrow{CB}$=$\frac{2}{3}$($\overrightarrow{AB}-\overrightarrow{AC}$)可得答案;
(2)延长CB到E,使BE=AG,连接AE,则$\overrightarrow{AE}$=$\overrightarrow{AG}+\overrightarrow{AB}$.
解答 解:(1)∵AG∥BC,AF=$\frac{2}{5}$AB,
∴△AGF∽△BCF,$\frac{AF}{BF}$=$\frac{2}{3}$,
∴$\frac{AG}{BC}$=$\frac{AF}{BF}$=$\frac{2}{3}$,即AG=$\frac{2}{3}$CB,
∴$\overrightarrow{AG}=\frac{2}{3}$$\overrightarrow{CB}$=$\frac{2}{3}$($\overrightarrow{AB}-\overrightarrow{AC}$)=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$;
(2)如图所示,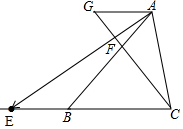
$\overrightarrow{AE}$=$\overrightarrow{BE}+\overrightarrow{AB}$=$\overrightarrow{AG}+\overrightarrow{AB}$.
点评 本题主要考查相似三角形的判定与性质及向量的运算、作图,熟练掌握向量的基本运算法则是解题的关键.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | -8 | D. | 8 |

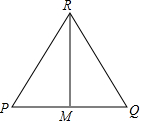 已知:如图,△RPQ中,RP=RQ,M为PQ的中点.
已知:如图,△RPQ中,RP=RQ,M为PQ的中点.