题目内容
7.(1)计算:$\sqrt{8}$+($\frac{1}{2}$)-1-(π+2)0+|1-$\sqrt{2}$|.(2)解方程 4x2-9=0.
分析 (1)直接利用负整数指数幂的性质以及零指数幂的性质和绝对值的性质分别化简求出答案;
(2)直接利用平方根的定义求出答案.
解答 解:(1)$\sqrt{8}$+($\frac{1}{2}$)-1-(π+2)0+|1-$\sqrt{2}$|
=2$\sqrt{2}$+2-1+$\sqrt{2}$-1
=3$\sqrt{2}$;
(2)4x2-9=0
则x2=$\frac{9}{4}$,
解得:x=±$\frac{3}{2}$.
点评 此题主要考查了实数运算以及平方根的应用,正确掌握相关运算法则是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏.
小明画出树状图如图所示:
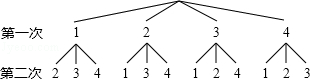
小华列出表格如下:
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后不放回(填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为(3,2);
(3)规定两次抽到的数字之和为奇数的获胜,按照各自的规则,你认为谁获胜的可能性大?说明理由?
小明画出树状图如图所示:

小华列出表格如下:
| 第一次 第二次 | 1 | 2 | 3 | 4 |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | ① | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) |
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后不放回(填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为(3,2);
(3)规定两次抽到的数字之和为奇数的获胜,按照各自的规则,你认为谁获胜的可能性大?说明理由?
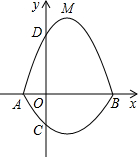 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线叫做“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=-x2+2x+3的顶点.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线叫做“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=-x2+2x+3的顶点. 已知抛物线y=-x2+bx+c的部分图象如图所示.
已知抛物线y=-x2+bx+c的部分图象如图所示. 如图,已知△ABC中,点F在边AB上,且AF=$\frac{2}{5}$AB、过A作AG∥BC交CF的延长线于点G.
如图,已知△ABC中,点F在边AB上,且AF=$\frac{2}{5}$AB、过A作AG∥BC交CF的延长线于点G.