题目内容
4．计算：（1）（$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{6}$）×2$\frac{2}{5}$
（2）|-$\frac{7}{9}$|÷（$\frac{2}{3}$-$\frac{1}{5}$）-$\frac{1}{3}$×（-4）2．
分析 （1）根据乘法分配律可以解答本题；
（2）根据有理数的乘除法和减法可以解答本题．
解答 解：（1）（$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{6}$）×2$\frac{2}{5}$
=$\frac{1}{3}×\frac{12}{5}-\frac{1}{4}×\frac{12}{5}+\frac{1}{6}×\frac{12}{5}$
=$\frac{4}{5}-\frac{3}{5}+\frac{2}{5}$
=$\frac{3}{5}$；
（2）|-$\frac{7}{9}$|÷（$\frac{2}{3}$-$\frac{1}{5}$）-$\frac{1}{3}$×（-4）2．
=$\frac{7}{9}÷\frac{7}{15}-\frac{1}{3}×16$
=$\frac{7}{9}×\frac{15}{7}-\frac{16}{3}$
=$\frac{5}{3}-\frac{16}{3}$
=-$\frac{11}{3}$．
点评 本题考查有理数的混合运算，解题的关键是明确有理数混合运算的计算方法．
练习册系列答案
相关题目
15．在不透明的袋子中有四张标着数字1，2，3，4的卡片，小明、小华两人按照各自的规则玩抽卡片游戏．
小明画出树状图如图所示：
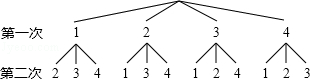
小华列出表格如下：
回答下列问题：
（1）根据小明画出的树形图分析，他的游戏规则是，随机抽出一张卡片后不放回（填“放回”或“不放回”），再随机抽出一张卡片；
（2）根据小华的游戏规则，表格中①表示的有序数对为（3，2）；
（3）规定两次抽到的数字之和为奇数的获胜，按照各自的规则，你认为谁获胜的可能性大？说明理由？
小明画出树状图如图所示：
小华列出表格如下：
| 第一次 第二次 | 1 | 2 | 3 | 4 |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） |
| 2 | （1，2） | （2，2） | ① | （4，2） |
| 3 | （1，3） | （2，3） | （3，3） | （4，3） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） |
（1）根据小明画出的树形图分析，他的游戏规则是，随机抽出一张卡片后不放回（填“放回”或“不放回”），再随机抽出一张卡片；
（2）根据小华的游戏规则，表格中①表示的有序数对为（3，2）；
（3）规定两次抽到的数字之和为奇数的获胜，按照各自的规则，你认为谁获胜的可能性大？说明理由？
已知抛物线y=-x2+bx+c的部分图象如图所示．
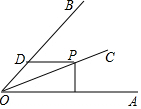如图，OC平分∠AOB=60°，且∠AOB=60°，点P为OC上任意点，PM⊥OA于M，PD∥OA，交OB于D，若OM=6，则PD的长为（ ）
如图，已知△ABC中，点F在边AB上，且AF=$\frac{2}{5}$AB、过A作AG∥BC交CF的延长线于点G．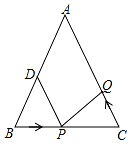
如图所示，已知△ABC中，AB=AC=10厘米，BC=8厘米，点D为AB的中点．如果点P在线段BC上以1厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动．