题目内容
6.(1)数轴上表示4和1的两点之间的距离是3;表示-3和2两点之间的距离是5;(2)一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|.如果表示数a和-2的两点之间的距离是4,那么a=2或-6;
(3)若此时数轴上有两点A,B对应的数分别为-30和20,如果点P沿线段AB自点A向B以每秒2个单位长度的速度运动,同时点Q沿线段BA自点B向A以每秒3个单位长度的速度运动,多长时间之后P,Q两点相遇?此时点P在数轴上对应的数是多少?

分析 (1)根据数轴,观察两点之间的距离即可解决;
(2)根据绝对值可得:a+2=±4,即可解答;
(3)设P、Q两点相遇所花的时间为t秒,根据等量关系:速度和×时间=路程和,列出方程求解即可.
解答 解:(1)数轴上表示4和1的两点之间的距离是:4-1=3;表示-3和2两点之间的距离是:2-(-3)=5;
(2)|a+2|=4,
a+2=4或a+2=-4,
a=2或x=-6.
(3)设P、Q两点相遇所花的时间为t秒,依题意得:
2t+3t=20-(-30),
t=10,
1×10=10.
答:P、Q两点经过10秒后相遇,此时点P在数轴上对应的数为-10.
故答案为:3,5;2或-6.
点评 此题考查数轴上两点之间的距离的算法:数轴上两点之间的距离等于相应两数差的绝对值,应牢记且会灵活应用.

练习册系列答案
相关题目
15.在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏.
小明画出树状图如图所示:
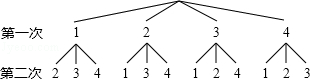
小华列出表格如下:
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后不放回(填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为(3,2);
(3)规定两次抽到的数字之和为奇数的获胜,按照各自的规则,你认为谁获胜的可能性大?说明理由?
小明画出树状图如图所示:

小华列出表格如下:
| 第一次 第二次 | 1 | 2 | 3 | 4 |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | ① | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) |
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后不放回(填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为(3,2);
(3)规定两次抽到的数字之和为奇数的获胜,按照各自的规则,你认为谁获胜的可能性大?说明理由?
 如图,CD⊥DE,AB⊥BF,AB=CD,AE=CF,求证:AB∥CD.
如图,CD⊥DE,AB⊥BF,AB=CD,AE=CF,求证:AB∥CD.
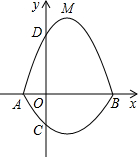 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线叫做“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=-x2+2x+3的顶点.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线叫做“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=-x2+2x+3的顶点. 如图,已知△ABC中,点F在边AB上,且AF=$\frac{2}{5}$AB、过A作AG∥BC交CF的延长线于点G.
如图,已知△ABC中,点F在边AB上,且AF=$\frac{2}{5}$AB、过A作AG∥BC交CF的延长线于点G.