题目内容
8.当x取什么数时,下列分式有意义?当x取什么数时,下列分式的值等于0?(1)$\frac{x}{{x}^{2}+0.1}$;
(2)$\frac{x-5}{{x}^{2}}$;
(3)$\frac{2|x|-10}{x-5}$.
分析 根据分母不为零分式有意义,分子为零且分母不为零分式的值为零,可得答案.
解答 解:(1)要使$\frac{x}{{x}^{2}+0.1}$有意义,得x2+0.1≠0.
x取任意实数,$\frac{x}{{x}^{2}+0.1}$有意义,x=0时,$\frac{x}{{x}^{2}+0.1}$=0;
(2)当x≠0时,$\frac{x-5}{{x}^{2}}$有意义,
当x-5=0时,即x=5时,$\frac{x-5}{{x}^{2}}$=0;
(3)当x≠5时,$\frac{2|x|-10}{x-5}$有意义,
当2|x|-10=0且x-5≠0时,即x=-5时,$\frac{2|x|-10}{x-5}$=0.
点评 本题考查了分式有意义的条件,分式无意义?分母为零;分式有意义?分母不为零;分式值为零?分子为零且分母不为零.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列各式正确的是( )
| A. | $\root{3}{216}$=±6 | B. | $\root{3}{(-5)^{3}}$=5 | C. | $\root{3}{(-11)^{3}}$=-11 | D. | $\root{3}{0.729}$=0.7 |
13.已知点A(3,m+1)在x轴上,点B(2-n,-2)在y轴上,则点C(m,n)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 已知:如图,AC=EC,E、A、D在同一条直线上,∠1=∠2=∠3.试说明:△ABC≌△EDC.
已知:如图,AC=EC,E、A、D在同一条直线上,∠1=∠2=∠3.试说明:△ABC≌△EDC.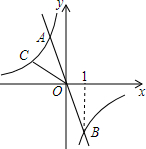 已知:如图,一次函数y1=-2x的图象与反比例函数${y_2}=\frac{k}{x}$的图象交于A、B两点,且点B的坐标为(1,m).
已知:如图,一次函数y1=-2x的图象与反比例函数${y_2}=\frac{k}{x}$的图象交于A、B两点,且点B的坐标为(1,m).