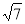Question

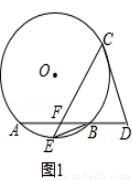
如图1，在⊙O中，E是弧AB的中点，C为⊙O上的一动点（C与E在AB异侧），连接EC交AB于点F，EB=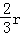（r是⊙O的半径）．

（1）D为AB延长线上一点，若DC=DF，证明：直线DC与⊙O相切；

（2）如图2，当F是AB的四等分点且EF·EC=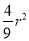时，求EC的值．

 

 

Answer 1

（1）详见解析；（2）EC=r

【解析】

试题分析：（1）证明：连结OC、OE，OE交AB于H，如图1，

∵E是弧AB的中点，∴OE⊥AB，∴∠EHF=90°，

∴∠HEF+∠HFE=90°，

而∠HFE=∠CFD，∴∠HEF+∠CFD=90°，

∵DC=DF，∴∠CFD=∠DCF，

而OC=OE，∴∠OCE=∠OEC，

∴∠OCE+∠DCE=∠HEF+∠CFD=90°，∴OC⊥CD，

∴直线DC与⊙O相切；

（2）【解析】
如图2，连结OA，

∵弧AE=弧BE，∴AE=BE=r，

设OH=x，则HE=r﹣x，

在Rt△OAH中，AH2+OH2=OA2，即AH2+x2=r2，

在Rt△EAH中，AH2+EH2=EA2，即AH2+（r﹣x）2=（r）2，

∴x2﹣（r﹣x）2=r2﹣（r）2，即得x=r，

∴HE=r﹣r=r，

在Rt△OAH中，AH===，

∵OE⊥AB，∴AH=BH，

而F是AB的四等分点，∴HF=AH=，

在Rt△EFH中，EF===r，

∵EF•EC=r2，∴r•EC=r2，∴EC=r．

考点：圆的综合运用