题目内容
已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
(1)如果用含a的代数式表示b,那么b= ;
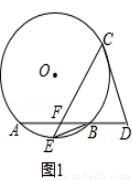
(2)如图所示,如果该图象与x轴的一个交点为(﹣1,0).

①求二次函数的表达式,并写出图象的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图象上所有等距点的坐标.
(3)当a取a1,a2时,二次函数图象与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a1和a2的大小.
(1)﹣a (2)①y=﹣x2+x+2,顶点坐标为;( ,
,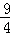 )②P1(
)②P1(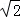 ,
,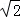 )、P2(
)、P2(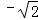 ,﹣
,﹣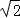 )、P3(1+
)、P3(1+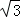 ,﹣1﹣
,﹣1﹣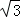 )、P4(1﹣
)、P4(1﹣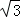 ,
,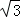 ﹣1)(3)a1<a2.
﹣1)(3)a1<a2.
【解析】
试题分析:(1)直接将点(1,2)代入抛物线的解析式中,即可得到a、b间的关系式.
(2)①已知抛物线图象上的两点坐标,且只有两个待定系数,利用待定系数法求解即可.
②P到x轴、y轴的距离相等,那么P点必在直线y=x或y=﹣x上,这两条直线与抛物线的交点,即为符合条件的等距点.
(3)首先根据(1)的结论,用a表示出函数的解析式,然后分别将M、N的坐标代入抛物线的解析式中,分别用m、n表示出a1、a2,通过做差可比较出a1、a2的大小.
试题解析:(1)将(1,2)代入y=ax2+bx+2中,得:
a+b+2=2,得:b=﹣a.
(2)①∵二次函数y=ax2+bx+c经过点(1,2)和(﹣1,0)
可得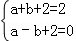 ,
,
解得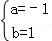 ,
,
即y=﹣x2+x+2,
顶点坐标为( ,
,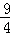 ).
).
②该函数图象上等距点的坐标即为此函数与函数y1=x和函数y2=﹣x的交点坐标
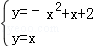 ,
,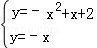 ,
,
解得P1(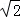 ,
,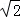 )、P2(
)、P2(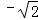 ,﹣
,﹣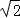 )、P3(1+
)、P3(1+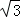 ,﹣1﹣
,﹣1﹣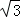 )、P4(1﹣
)、P4(1﹣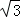 ,
,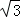 ﹣1).
﹣1).
(3)∵二次函数与x轴正半轴交于点(m,0)且a=﹣b,
∴a1m2﹣a1m+2=0,即 a1=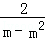 ,
,
同理 a2n2﹣a2n+2=0,a2=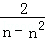 ,
,
故 a2﹣a1=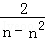 ﹣
﹣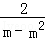 =
=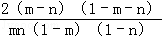 ,
,
∵n>m>1,故 a2﹣a1=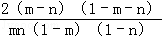 >0,
>0,
∴a1<a2.
考点:二次函数综合题.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案