题目内容
3.直线y=2x+2交抛物线y=x2于点A,B,O为原点,则△ABO的面积为8.分析 根据题意可以分别求得点A和点B的坐标,然后将x=0代入y=2x+2,可以求得直线y=2x+2与y轴的交点,从而可以求得△ABO的面积.
解答 解:由题意可得,
$\left\{\begin{array}{l}{y=2x+2}\\{y={x}^{2}}\end{array}\right.$,
解得,${x}_{1}=1-\sqrt{3}$,${x}_{2}=1+\sqrt{3}$,
∴点A的坐标为($1-\sqrt{3}$,4$-2\sqrt{3}$),点B的坐标为(1$+\sqrt{3}$,$4+2\sqrt{3}$),
将x=0代入y=2x+2,得y=2,
∴△ABO的面积为:$\frac{2×(4-2\sqrt{3})}{2}+\frac{2×(4+2\sqrt{3})}{2}$=8,
故答案为:8.
点评 本题考查二次函数图象上点的坐标特征、一次函数图象上点的坐标特征、三角形的面积,解答此类问题的关键是求出直线与抛物线的交点,利用三角形的面积公式解答.

练习册系列答案
相关题目
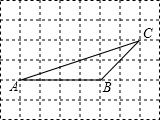 如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点)
如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点) 以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A、B分别作⊙C的切线,E,D为切点,
以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A、B分别作⊙C的切线,E,D为切点, 如图,在线段BF上,有点E、C,BE=CF,∠B=∠F,∠ACB=∠DEF.
如图,在线段BF上,有点E、C,BE=CF,∠B=∠F,∠ACB=∠DEF.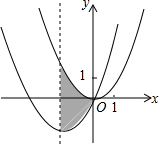 如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.
如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.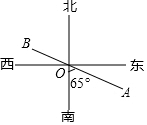 如图,直线AB经过点O,根据图形解答下列问题:
如图,直线AB经过点O,根据图形解答下列问题: