题目内容
19.解方程组$\left\{\begin{array}{l}{x+y=4.①}\\{\frac{x+y}{3}-\frac{x}{2}=1.②}\end{array}\right.$.分析 首先去分母化简方程组,然后选择正确的方法进行消元.
解答 解:②化简得-x+2y=6③,
①+③得3y=10,
解得y=$\frac{10}{3}$,
把xy=$\frac{10}{3}$代入①,得$\frac{10}{3}$+y=4,
解得x=$\frac{2}{3}$.
故原方程组的解为$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{10}{3}}\end{array}\right.$.
点评 本题考查了解二元一次方程组,方程组中的方程不是最简方程的,最好是先化成最简方程,再选择合适的方法解方程组.

练习册系列答案
相关题目
11.下列各式中,属于最简二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{4}$ | C. | $\sqrt{8}$ | D. | $\sqrt{10}$ |
10.某市深入实施环境污染整治,去年排放的污水减少了30万吨,将30万用科学记数法表示为( )
| A. | 3.0×105 | B. | 30×104 | C. | 3.0×104 | D. | 3.0×101 |
7.下列各式能用平方差公式进行计算的是( )
| A. | (x-3)(x+1) | B. | (a+2b)(2a-b) | C. | (-a+1)(-a-1) | D. | (x-3)2 |
 如图所示,∠1=∠DBF,∠3=∠4,且BD=BF
如图所示,∠1=∠DBF,∠3=∠4,且BD=BF 的图象,其对称轴为x=1,下列结论:①
的图象,其对称轴为x=1,下列结论:①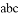 >0;②
>0;②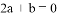 ;③
;③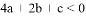 ;④若
;④若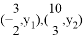 是抛物线上两点,则y1<y2其中结论正确的是( )
是抛物线上两点,则y1<y2其中结论正确的是( )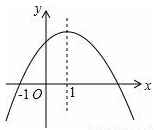
 的两根,则k的值为______.
的两根,则k的值为______.