题目内容
11.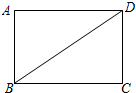 如图所示,BD是矩形ABCD的对角线.
如图所示,BD是矩形ABCD的对角线.(1)请用尺规作图:作△BC′D与△BCD关于矩形ABCD的对角线BD所在的直线对称(要求:不写作法,不证明,保留作图痕迹).
(2)若矩形ABCD的边AB=6,BC=8,(1)中BC′交AD于点E,求线段BE的长.
分析 (1)利用过直线外一点作已知直线的垂线的方法作BD的垂线,然后再确定C关于BD的对称点C′,再连接BC′、DC′即可;
(2)首先证明BE=DE,再表示出AE长,然后利用勾股定理可得方程62+(8-BE)2=BE2,再解即可.
解答 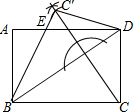 解:(1)如右图所示:
解:(1)如右图所示:
(2)由(1)知,∠CBD=∠EBD,
又∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
又∵AD=8,
∴AE=8-DE=8-BE,
在Rt△ABE中有,62+(8-BE)2=BE2,
解方程得:BE=$\frac{25}{4}$.
点评 此题主要考查了作图--轴对称变换,以及勾股定理得应用,关键是正确画出图形,利用等角对等边得到EB=ED.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
1.4的平方根是( )
| A. | 4 | B. | -4 | C. | 2 | D. | ±2 |
19.下列命题中,是真命题的是( )
| A. | 周长相等的等边三角形都全等 | |
| B. | 周长相等的直角三角形都全等 | |
| C. | 如果两个三角形的两边及其中一边的对角对应相等,则这两个三角形全等 | |
| D. | 如果两个三角形的三个角对应相等,则这两个三角形全等 |
 如图所示,在△ABC中,AC=9cm,DE垂直平分AB,如果△DBC的周长是16cm,那么BC的长度为7cm.
如图所示,在△ABC中,AC=9cm,DE垂直平分AB,如果△DBC的周长是16cm,那么BC的长度为7cm. 如图,∠ACE=∠BCF,请补充一个条件:∠A=∠E(答案不唯一),使△ACB∽△ECF.
如图,∠ACE=∠BCF,请补充一个条件:∠A=∠E(答案不唯一),使△ACB∽△ECF. 如图,已知线段AB.用尺规作图的方法作出线段AB的垂直平分线(保留作图痕迹,不要求写出作法).
如图,已知线段AB.用尺规作图的方法作出线段AB的垂直平分线(保留作图痕迹,不要求写出作法).