题目内容
2.已知二次函数y=(m-1)x2+2mx+m+3,当该抛物线都在x轴上方时,求m的范围.分析 根据题意,抛物线开口向上,抛物线与x轴没有公共点,于是根据二次函数的性质和判别式的意义得到m-1>0且△=4m2-4(m-1)(m+3)<0,然后解不等式求出两不等式的公共部分即可.
解答 解:∵抛物线都在x轴上方,
∴m-1>0且△=4m2-4(m-1)(m+3)<0,
∴m>$\frac{3}{2}$.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.两个相似三角形的相似比为1:2,则它们周长的比为( )
| A. | 1:4 | B. | 1:2 | C. | $\sqrt{2}$ | D. | 4 |
17.若二次函数y=x2-4x+k的图象经过点(-1,y1),(3,y2),则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
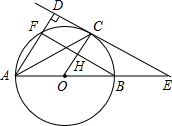 如图.AB是⊙O的直径.C是⊙O上的一点.直线CE与AB的延长线相交于点E,已AD⊥CE,垂足为D.AD交⊙O于点F,AC平分∠DAE.
如图.AB是⊙O的直径.C是⊙O上的一点.直线CE与AB的延长线相交于点E,已AD⊥CE,垂足为D.AD交⊙O于点F,AC平分∠DAE. 如图,⊙O中,弦AD=BC.
如图,⊙O中,弦AD=BC.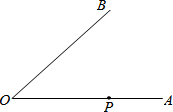 已知∠AOB和OA边上的一点P,如图,求作一点M,使M到∠AOB两边的距离相等且PM⊥OA.(要求:尺规作图,不写作法,但保留作图痕迹)
已知∠AOB和OA边上的一点P,如图,求作一点M,使M到∠AOB两边的距离相等且PM⊥OA.(要求:尺规作图,不写作法,但保留作图痕迹)