题目内容
 已知点A在数轴上对应的数为a,点B对应的数为b,A、B之间的距离记作AB,定义:AB=|a-b|,且|a+2|+(b-5)2=0.
已知点A在数轴上对应的数为a,点B对应的数为b,A、B之间的距离记作AB,定义:AB=|a-b|,且|a+2|+(b-5)2=0.(1)求线段AB的长;
(2)设点P在数轴上对应的数为x,当PA+PB=10时,求x的值;
(3)如图,M、N两点分别从O、B出发以v1、v2的速度同时沿数轴负方向运动(M在线段AO上,N在线段BO上),P是线段AN的中点,若M、N运动到任一时刻时,总有PM为定值,下列结论:①
| v1 |
| v2 |
考点:一元一次方程的应用,数轴,绝对值
专题:
分析:(1)根据非负数的和为0,各项都为0即可求解;
(2)应考虑到A、B、P三点之间的位置关系的多种可能解题;
(3)先求出PM=AP-AM=1.5-
v2t+v1t,根据M、N运动到任一时刻时,总有PM为定值,而t=0时,PM=1.5;t=1时,PM=1.5-
v2+v1;t=2时,PM=1.5-v2+2v1;得出1.5-v2+2v1=1.5-
v2+v1=1.5,整理得到
=
,即
的值不变,值为
.
(2)应考虑到A、B、P三点之间的位置关系的多种可能解题;
(3)先求出PM=AP-AM=1.5-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v1 |
| v2 |
| 1 |
| 2 |
| v1 |
| v2 |
| 1 |
| 2 |
解答: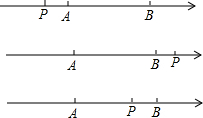 解:(1)∵|a+2|+(b-5)2=0,
解:(1)∵|a+2|+(b-5)2=0,
∴a=-2,b=5,
∴AB=|a-b|=7,即线段AB的长度为7.
(2)当P在点A左侧时.PA+PB=(-2-x)+(-x+5)=10,即-2x+7=10,解得 x=-3.5;
当点P在点B的右侧时,PA+PB=(x+2)+(x-5)=10,即2x-3=10,解得 x=6.5;
当点P在点A与B之间时,PA+PB=x+2+5-x=10,不存在这样的x的值.
综上所述,x的值是-3.5或6.5;
(3)①
的值不变.理由如下:
∵ PM=AP-AM
PM=AP-AM
=
AN-(OA-OM)
=
(AB-BN)-OA+OM
=
(7-v2t)-2+v1t
=1.5-
v2t+v1t,
∵M、N运动到任一时刻时,总有PM为定值,
而t=0时,PM=1.5,
t=1时,PM=1.5-
v2+v1,
t=2时,PM=1.5-v2+2v1,
∴1.5-v2+2v1=1.5-
v2+v1=1.5,
∴
=
,
即
的值不变,值为
.
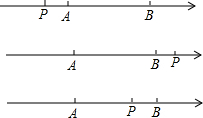 解:(1)∵|a+2|+(b-5)2=0,
解:(1)∵|a+2|+(b-5)2=0,∴a=-2,b=5,
∴AB=|a-b|=7,即线段AB的长度为7.
(2)当P在点A左侧时.PA+PB=(-2-x)+(-x+5)=10,即-2x+7=10,解得 x=-3.5;
当点P在点B的右侧时,PA+PB=(x+2)+(x-5)=10,即2x-3=10,解得 x=6.5;
当点P在点A与B之间时,PA+PB=x+2+5-x=10,不存在这样的x的值.
综上所述,x的值是-3.5或6.5;
(3)①
| v1 |
| v2 |
∵
 PM=AP-AM
PM=AP-AM=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=1.5-
| 1 |
| 2 |
∵M、N运动到任一时刻时,总有PM为定值,
而t=0时,PM=1.5,
t=1时,PM=1.5-
| 1 |
| 2 |
t=2时,PM=1.5-v2+2v1,
∴1.5-v2+2v1=1.5-
| 1 |
| 2 |
∴
| v1 |
| v2 |
| 1 |
| 2 |
即
| v1 |
| v2 |
| 1 |
| 2 |
点评:此题主要考查了一元一次方程的应用,渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则△OBC的周长为( )
如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则△OBC的周长为( )| A、12cm | B、13cm |
| C、14cm | D、16cm |
长方形的一边等于2a+3b,另一边比它大a-b,则此长方形的周长为( )
| A、10a+10b |
| B、6a+4b |
| C、4a+6b |
| D、3a+2b |
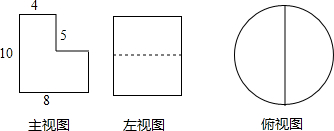 一个几何体的三视图如图所示,你能画出这个几何体吗?并求出它的表面积和体积.
一个几何体的三视图如图所示,你能画出这个几何体吗?并求出它的表面积和体积. 如图,将两个含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
如图,将两个含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗? 如图,已知∠1+∠2=180°,∠3=∠B,∠4=40°,求∠ACB的度数.
如图,已知∠1+∠2=180°,∠3=∠B,∠4=40°,求∠ACB的度数.