题目内容
已知x是一元二次方程x2-8x-3=0的实数根,求代数式
÷(x+3-
)的值.
| x+4 |
| x2-7x+12 |
| 7 |
| x-3 |
考点:分式的化简求值,一元二次方程的解
专题:
分析:先根据分式混合运算的法则把原式进行化简,再根据x是一元二次方程x2-8x-3=0的实数根得出x2-8x=3,再代入原式进行计算即可.
解答:解:原式=
÷
=
÷
=
•
=
=
,
∵x是一元二次方程x2-8x-3=0的实数根,
∴x2-8x=3,
∴原式=
=
.
| x+4 |
| (x-3)(x-4) |
| x2-9-7 |
| x-3 |
=
| x+4 |
| (x-3)(x-4) |
| (x-4)(x+4) |
| x-3 |
=
| x+4 |
| (x-3)(x-4) |
| x-3 |
| (x-4)(x+4) |
=
| 1 |
| (x-4)2 |
=
| 1 |
| x2-8x+16 |
∵x是一元二次方程x2-8x-3=0的实数根,
∴x2-8x=3,
∴原式=
| 1 |
| 3+16 |
| 1 |
| 19 |
点评:本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
一个三角形的两边长分别为4cm和8cm,则此三角形的第三边的长可能是( )
| A、3cm | B、4cm |
| C、9cm | D、13cm |
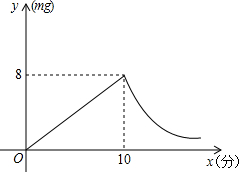 为预防“手足口病”,某校对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量为y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.根据以上信息,解答下列问题:
为预防“手足口病”,某校对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量为y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.根据以上信息,解答下列问题: 已知点A在数轴上对应的数为a,点B对应的数为b,A、B之间的距离记作AB,定义:AB=|a-b|,且|a+2|+(b-5)2=0.
已知点A在数轴上对应的数为a,点B对应的数为b,A、B之间的距离记作AB,定义:AB=|a-b|,且|a+2|+(b-5)2=0.