题目内容
4.若实数a、b满足|a+b|+$\sqrt{b-2}$=0,则$\frac{{a}^{2}}{b}$=2.分析 本题可根据分式值为0和非负数的性质求出a、b的值,代入代数式即可得到结论.
解答 解:∵|a+b|+$\sqrt{b-2}$=0,
∴a+b=0,b-2=0,
∴a=-2,b=2,
∴$\frac{{a}^{2}}{b}$=2,
故答案为:2.
点评 本题考查了非负数的性质,两个非负数相加,和为0,这两个非负数的值都为0.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
12. 如图,已知a、b、c、d四条直线,a∥b,c∥d,∠1=112°,则∠2等于( )
如图,已知a、b、c、d四条直线,a∥b,c∥d,∠1=112°,则∠2等于( )
 如图,已知a、b、c、d四条直线,a∥b,c∥d,∠1=112°,则∠2等于( )
如图,已知a、b、c、d四条直线,a∥b,c∥d,∠1=112°,则∠2等于( )| A. | 58° | B. | 68° | C. | 78° | D. | 112° |
19.若把分式$\frac{2xy}{3x-y}$的x、y同时扩大为原来的3倍,则分式的值( )
| A. | 扩大3倍 | B. | 缩小3倍 | C. | 不变 | D. | 缩小6倍 |
 如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A,B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=$\frac{3}{4}$x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A,B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=$\frac{3}{4}$x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.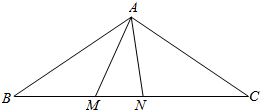 如图,△ABC中,AB=AC,∠B=36°,M,N是BC上两点,且∠AMN=∠ANM=2∠BAM,则图中的等腰三角形一共有( )
如图,△ABC中,AB=AC,∠B=36°,M,N是BC上两点,且∠AMN=∠ANM=2∠BAM,则图中的等腰三角形一共有( )