题目内容
 如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.(1)判断四边形ACED的形状,并说明理由;
(2)若BD=
| 2 |
考点:正方形的性质,勾股定理,平行四边形的判定
专题:
分析:(1)根据正方形的对边互相平行可得AD∥BC,即为AD∥CE,然后根据两组对边互相平行的四边形是平行四边形解答;
(2)根据正方形的四条边都相等,平行四边形的对边相等可得BC=AD=CE,再根据正方形的边长等于对角线的
倍求出BC,然后求出BE即可.
(2)根据正方形的四条边都相等,平行四边形的对边相等可得BC=AD=CE,再根据正方形的边长等于对角线的
| ||
| 2 |
解答:解:(1)四边形ACED是平行四边形.理由如下:
∵四边形ABCD是正方形,
∴AD∥BC,即AD∥CE.
∵DE∥AC,
∴四边形ACED是平行四边形;
(2)由(1)知,BC=AD=CE=CD,
∵BD=
,
∴BC=
BD=
×
=1,
∴BE=BC+CE=1+1=2.
∵四边形ABCD是正方形,
∴AD∥BC,即AD∥CE.
∵DE∥AC,
∴四边形ACED是平行四边形;
(2)由(1)知,BC=AD=CE=CD,
∵BD=
| 2 |
∴BC=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴BE=BC+CE=1+1=2.
点评:本题考查了正方形的性质,平行四边形的判定与性质,比较简单,熟练掌握各图形的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
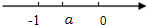 实数a在数轴上的位置如图,则a,-a,
实数a在数轴上的位置如图,则a,-a,| 1 |
| a |
A、a<-a<
| ||
B、-a<
| ||
C、
| ||
D、
|
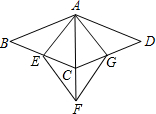 小明设计了一个如图的风筝,其中,四边形ABCD与四边形AEFG都是菱形,点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,AE=100cm,求菱形ABCD的边长.
小明设计了一个如图的风筝,其中,四边形ABCD与四边形AEFG都是菱形,点C在AF上,点E,G分别在BC,CD上,若∠BAD=135°,∠EAG=75°,AE=100cm,求菱形ABCD的边长. 如图,在?ABCD中,点E、点F分别在AD、CB的延长线上,且DE=BF,连结EF分别交AB、CD于点H、点G.
如图,在?ABCD中,点E、点F分别在AD、CB的延长线上,且DE=BF,连结EF分别交AB、CD于点H、点G.