题目内容
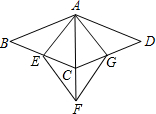小明设计了一个如图的风筝，其中，四边形ABCD与四边形AEFG都是菱形，点C在AF上，点E，G分别在BC，CD上，若∠BAD=135°，∠EAG=75°，AE=100cm，求菱形ABCD的边长．考点：菱形的性质
专题：
分析：根据菱形的性质可得出∠BAE=30°，∠B=45°，过点E作EM⊥AB于点M，设EM=x，则可得出AB、AE的长度，继而可得出
的值，求出AB即可．
| AB |
| AE |
解答：
解：∵∠BAD=135°，∠EAG=75°，四边形ABCD与四边形AEFG都是菱形，
∴∠B=180°-∠BAD=45°，∠BAE=∠BAC-∠EAC=30°，
过点E作EM⊥AB于点M，设EM=x，
在Rt△AEM中，AE=2EM=2x，AM=
x，
在Rt△BEM中，BM=x，
则
=
=
，
∵AE=100cm，∴AB=50（
+1）cm，
∴菱形ABCD的边长为：50（
+1）cm．
解：∵∠BAD=135°，∠EAG=75°，四边形ABCD与四边形AEFG都是菱形，∴∠B=180°-∠BAD=45°，∠BAE=∠BAC-∠EAC=30°，
过点E作EM⊥AB于点M，设EM=x，
在Rt△AEM中，AE=2EM=2x，AM=
| 3 |
在Rt△BEM中，BM=x，
则
| AB |
| AE |
| AM+BM |
| AE |
| ||
| 2 |
∵AE=100cm，∴AB=50（
| 3 |
∴菱形ABCD的边长为：50（
| 3 |
点评：本题考查了菱形的性质及解直角三角形的知识，属于基础题，关键是掌握菱形的对角线平分一组对角．
练习册系列答案
教材全解字词句篇系列答案
相关题目
已知一次函数y=kx+1的图象过点（1，3），则k的值为（ ）
| A、1 | ||
| B、2 | ||
| C、-1 | ||
D、
|
化简：-
=（ ）
| 4 |
| A、2 | B、-2 | C、4 | D、-4 |
如图，过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E．
如图，已知?ABCD．