题目内容
18.已知:菱形的边长为4,且有一个内角为60°,一条直线将菱形ABCD分成面积相等的两个图形,设该直线与菱形的边交于点E,F,则线段EF的长m的取值范围( )| A. | m=4或m=4$\sqrt{3}$ | B. | 4≤m≤4$\sqrt{3}$ | C. | 2$\sqrt{3}$≤m≤4$\sqrt{3}$ | D. | 2$\sqrt{3}$≤m≤4 |
分析 由题目所提供的材料信息可知当菱形的线段EF和边垂直时最小,当线段EF为菱形的对角线时最大,由此可得问题答案.
解答 解:由题意当线段EF和边垂直时最小,
此时直线l⊥DC,过点D作DN⊥AB于点N,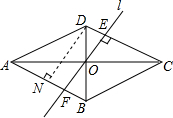
则∠DAB=60°,AD=4,
故DN=AD•sin60°=2 $\sqrt{3}$,
当线段EF为菱形的对角线时最大,
则DO=2,故AO=2 $\sqrt{3}$,即AC=4 $\sqrt{3}$,
则m的取值范围是:2 $\sqrt{3}$≤m≤4 $\sqrt{3}$.
故选C.
点评 本题考查了菱形的性质以及勾股定理的运用,读懂题意,弄明白”等积线段”的定义,并准确判断出最短与最长的“等积线段”是解题的关键.

练习册系列答案
相关题目
14.下列说法中,正确的是( )
| A. | 一组数据-2,-1,0,1,1,2的中位数是0 | |
| B. | 质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式 | |
| C. | 购买一张福利彩票中奖是一个确定事件 | |
| D. | 分别写有三个数字-1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为$\frac{1}{3}$ |
 如图,已知AB∥CD,∠1=140°,则∠2=40°.
如图,已知AB∥CD,∠1=140°,则∠2=40°. 如图,已知点O为平行四边形ABCD所在平面上一点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,求$\overrightarrow{OD}$(用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,已知点O为平行四边形ABCD所在平面上一点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,求$\overrightarrow{OD}$(用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示) 解不等式组$\left\{\begin{array}{l}{5x-2≥3(x-1)}\\{\frac{1}{2}x-1<5-\frac{3}{2}x}\end{array}\right.$,并把解集在所给数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{5x-2≥3(x-1)}\\{\frac{1}{2}x-1<5-\frac{3}{2}x}\end{array}\right.$,并把解集在所给数轴上表示出来.