题目内容
19.手工课上,小明准备做个形状是菱形的风筝,这个菱形两条对角线长度之和恰好为60cm,菱形的面积为S,随其中一条对角线的长x的变化而变化.①求S与x之间的函数关系式(不要求写出取值范围)
②当x是多少时,菱形风筝的面积S最大?最大的面积是多少?
分析 ①首先表示出菱形对角线的长,再利用菱形面积求法得出答案;
②利用配方法求出二次函数最值即可.
解答 解:①根据题意可得:一条对角线的长为xcm,则另一对角线长为:(60-x),
则S=$\frac{1}{2}$x(60-x)=-$\frac{1}{2}$x2+30x;
②由①得:S=-$\frac{1}{2}$x2+30x=-$\frac{1}{2}$(x-30)2+450,
故当x是30cm时,菱形风筝的面积S最大,最大的面积是450cm2.
点评 此题主要考查了二次函数的应用,根据题意结合菱形的性质得出y与x之间的关系式是解题关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
10.下列代数式中符合书写要求的是( )
| A. | ab2×4 | B. | xy2÷3 | C. | $\frac{1}{4}xy$ | D. | $2\frac{1}{2}{a^2}b$ |
4.在平面直角坐标系中,点A(-2,-3)在( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
9.在平面直角坐标系中,以点A(2,4)为圆心,1为半径作⊙A,以点B(3,5)为圆心,3为半径作⊙B,M、N分别是⊙A,⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为( )
| A. | $\sqrt{82}$-4 | B. | $\sqrt{82}$-1 | C. | 6-2$\sqrt{2}$ | D. | $\sqrt{17}$-3 |
 如图,在△ABC中,AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
如图,在△ABC中,AB=AC,D是AC上的一点,CD=9,BC=15,BD=12. 如图,A、B两村和一条小河,要在河边L建一水厂Q向两村供水,若要使自来水厂到两村的输水管用料最省,厂址Q应选在哪个位置?请将上述情况下的自来水厂厂址标出,并保留作图痕迹.
如图,A、B两村和一条小河,要在河边L建一水厂Q向两村供水,若要使自来水厂到两村的输水管用料最省,厂址Q应选在哪个位置?请将上述情况下的自来水厂厂址标出,并保留作图痕迹.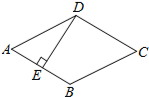 如图,菱形ABCD中,E是AB中点,DE⊥AB,则∠ADC的度数为120°.
如图,菱形ABCD中,E是AB中点,DE⊥AB,则∠ADC的度数为120°. 如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,那么CB的长是多少?
如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,那么CB的长是多少?