题目内容
17．已知在平面直角坐标系中，点A（a-3，-5）与点B（1，b+7）关于x轴对称，则$\sqrt{2a-3b}$的值为（精确到0.1）（ ）| A． | 3.4 | B． | 3.5 | C． | 3.6 | D． | 3.7 |
分析 直接利用关于x轴对称点的性质得出a，b的值，进而求出答案．
解答 解：∵点A（a-3，-5）与点B（1，b+7）关于x轴对称，
∴a-3=1，b+7=5，
解得：a=4，b=-2，
则$\sqrt{2a-3b}$=$\sqrt{2×4-3×（-2）}$=$\sqrt{14}$≈3.7．
故选：D．
点评 此题主要考查了关于x轴对称点的性质，正确得出a，b的值是解题关键．
练习册系列答案
相关题目
7．已知三点（x1，y1）、（x2，y2）、（x3，y3）均在双曲线y=$\frac{4}{x}$上，且x1＜x2＜0＜x3，则下列各式正确的是（ ）
| A． | y1＜y2＜y3 | B． | y3＜y2＜y1 | C． | y3＜y1＜y2 | D． | y2＜y1＜y3 |
8．
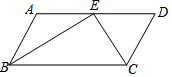如图，平行四边形ABCD中，∠ABC和∠BCD的平分线交于AD边上一点E，且BE=5，CE=4，则AB的长是（ ）
如图，平行四边形ABCD中，∠ABC和∠BCD的平分线交于AD边上一点E，且BE=5，CE=4，则AB的长是（ ）| A． | $\frac{{\sqrt{41}}}{2}$ | B． | 5 | C． | $\sqrt{29}$ | D． | 3 |
2．
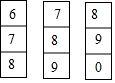如图是鹏鹏存钱罐的密码锁（每个密码都是0-9中的一个数），该密码锁的一个密码是7，后两位的密码鹏鹏记不清了，他只记得后两位的密码都比6大，则鹏鹏第一次就能打开改密码锁的概率是（ ）
如图是鹏鹏存钱罐的密码锁（每个密码都是0-9中的一个数），该密码锁的一个密码是7，后两位的密码鹏鹏记不清了，他只记得后两位的密码都比6大，则鹏鹏第一次就能打开改密码锁的概率是（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{8}$ | D． | $\frac{1}{9}$ |
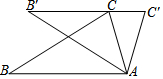如图，把△ABC绕着点A顺时针方向旋转32°，得到△AB'C'，恰好B'，C，C'三点在一直线上，则么∠C'=74°．