题目内容
19．
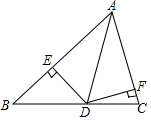如图，AD是△ABC角平分线，DE⊥AB，DF⊥AC，垂足分别为点E和点F，则下列结论正确的是（ ）| A． | BD=CD | B． | AD=BD | C． | AD=CD | D． | DE=DF |
分析 直接根据角平分线的性质进行判断．
解答 解：∵AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，
∴DE=DF．
故选D．
点评 本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．也考查了角平分线的性质．
练习册系列答案
相关题目
9．
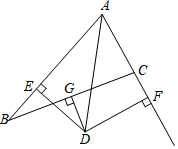如图，在△ABC中，AB=7，AC=3，G为BC的中点，DG⊥BC交∠BAC的平分线AD于D，DE⊥AB于E，DF⊥AC于F交AC的延长线于F，下列说法正确的是（ ）
①△ADE≌△ADF；②BE=CF；③AE=5．
如图，在△ABC中，AB=7，AC=3，G为BC的中点，DG⊥BC交∠BAC的平分线AD于D，DE⊥AB于E，DF⊥AC于F交AC的延长线于F，下列说法正确的是（ ）①△ADE≌△ADF；②BE=CF；③AE=5．
| A． | ①② | B． | ①③ | C． | ②③ | D． | ①②③ |
7．
如图是正方体的展开图，则原正方体相对的面上的数字和的最小值是（ ）
如图是正方体的展开图，则原正方体相对的面上的数字和的最小值是（ ）| A． | -4 | B． | 1 | C． | -6 | D． | 2 |
14．三角形的外心是三角形的（ ）
| A． | 三条中线的交点 | B． | 三条中垂线的交点 | ||
| C． | 三条高的交点 | D． | 三条角平分线的交点 |
4．已知-4x＞3，则下列不等式中，错误的是（ ）
| A． | -4x+1＞4 | B． | -4x-3＞0 | C． | x＞-$\frac{3}{4}$ | D． | -$\frac{4}{3}$x＞1 |
11．在$\frac{1}{3}$ab-$\frac{1}{4}$ac、$\frac{x}{x+y}$、$\frac{1}{π}$、1-$\frac{1}{x}$中，分式的个数有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
8．在-2，$\sqrt{4}$，$\sqrt{2}$，3.14这4个数中，无理数是（ ）
| A． | -2 | B． | $\sqrt{4}$ | C． | $\sqrt{2}$ | D． | 3.14 |