题目内容
8.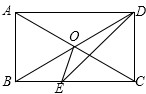 如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
分析 (1)只要证明三个角是直角即可解决问题;
(2)作OF⊥BC于F.求出EC、OF的长即可;
解答 (1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=90°,
∴∠BAD=90°,
∴∠BAD=∠ABC=∠ADC=90°,
∴四边形ABCD是矩形.
(2)作OF⊥BC于F.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=$\frac{1}{2}$CD=1,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△OEC的面积=$\frac{1}{2}$•EC•OF=1.
点评 本题考查矩形的判定和性质、角平分线的定义、三角形中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形中位线解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列运算中,正确的是( )
| A. | a3+a3=2a6 | B. | a5-a3=a2 | C. | a2•a2=2a4 | D. | (a5)2=a10 |
13.若a2-2a-3=0,代数式$\frac{1}{a(a-2)}$的值是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
2.某辆汽车油箱剩余油量z(L)与其形式路程x(km)之间的关系如下表所示,则这辆汽车耗油量y(L)与汽车行驶路程x(km)之间的关系式为y=$\frac{3}{50}$x
| 汽车行驶路程x(km) | 0 | 50 | 100 | 150 | 200 |
| 油箱剩余油量z(L) | 45 | 42 | 39 | 36 | 33 |
 如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)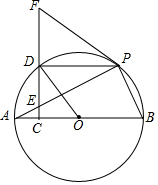 如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.
如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.