题目内容
13. 如图,在△ABC中,∠ACB=90°,CD⊥AB于D点,AB=5,CD=2,则△ABC的周长是3$\sqrt{5}$+5.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D点,AB=5,CD=2,则△ABC的周长是3$\sqrt{5}$+5.
分析 根据三角形的面积公式求出AC×BC=10,根据完全平方公式、勾股定理求出AC+BC,根据三角形的周长公式计算即可.
解答 解:$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×AB×CD,
∴AC×BC=10,
∵AC2+BC2=AB2,
∴(AC+BC)2=AB2+2×AC×BC=45,
∴AC+BC=3$\sqrt{5}$,
则AB+AC+BC=5+3$\sqrt{5}$,
∴△ABC的周长是3$\sqrt{5}$+5,
故答案为:3$\sqrt{5}$+5.
点评 本题考查的是勾股定理的应用,掌握如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.

练习册系列答案
相关题目
2.某辆汽车油箱剩余油量z(L)与其形式路程x(km)之间的关系如下表所示,则这辆汽车耗油量y(L)与汽车行驶路程x(km)之间的关系式为y=$\frac{3}{50}$x
| 汽车行驶路程x(km) | 0 | 50 | 100 | 150 | 200 |
| 油箱剩余油量z(L) | 45 | 42 | 39 | 36 | 33 |
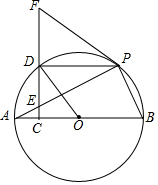 如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.
如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.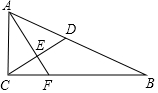 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在AB上,AD=AC,AF⊥CD交CD于点E,交BC于点F,则CF=$\frac{10}{3}$.
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在AB上,AD=AC,AF⊥CD交CD于点E,交BC于点F,则CF=$\frac{10}{3}$.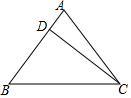 如图,等腰△ABC的底边BC=20cm,D是AB边上的一点,CD=16cm,BD=12cm,求△ABC的面积.
如图,等腰△ABC的底边BC=20cm,D是AB边上的一点,CD=16cm,BD=12cm,求△ABC的面积.