题目内容
19.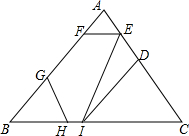 如图,D,E,F,G,H,I是三角形ABC三边上的点,连结EI,EF∥BC,GH∥AC,DI∥AB.
如图,D,E,F,G,H,I是三角形ABC三边上的点,连结EI,EF∥BC,GH∥AC,DI∥AB.(1)写出与∠IEC是同旁内角的角.
(2)判断∠GHC与∠FEC是否相等,并说明理由.
(3)若EI平分∠FEC,∠C=56°,∠B=50°,求∠EID的度数.
分析 (1)根据同旁内角的定义解答即可;
(2)根据平行线的性质得到∠FEC+∠C=180°,∠GHC+∠C=180°,根据余角的性质即可得到结论;
(3)根据平行线的性质得到∠FEC+∠C=180°,求得∠FEC=180°-∠C=124°,根据角平分线的定义得到∠FEI=$\frac{1}{2}$∠FEC=62°,由平行线的性质得到∠DIC=∠B=50°,即可得到结论.
解答 解:(1)与∠IEC是同旁内角的角是:∠C、∠EDI、∠EIC、∠EID;
(2)∠GHC=∠FEC,
理由:∵EF∥BC,
∴∠FEC+∠C=180°,
∵GH∥AC,
∴∠GHC+∠C=180°,
∴∠GHC=∠FEC;
(3)∵EF∥BC,∠C=56°,
∴∠FEC+∠C=180°,
∴∠FEC=180°-∠C=124°,
∵EI平分∠FEC,
∴∠FEI=$\frac{1}{2}$∠FEC=62°,
∴∠FEI=∠EIC=62°,
∵DI∥AB,∠B=50°,
∴∠DIC=∠B=50°,
∴∠EID=∠EIC-∠DIC=12°.
点评 本题考查了平行线的性质,角平分线的定义,同旁内角的定义,熟练掌握平行线的性质是解题的关键.

练习册系列答案
相关题目
7.下列给出的算式中,你认为可以帮助探究有理数加法法则的算式组合是( )
①3+(-2);②4+3;③(-3)+(-2);④3+13;⑤3+0;⑥6+(-3);⑦4+(-5);⑧5+(-5).
①3+(-2);②4+3;③(-3)+(-2);④3+13;⑤3+0;⑥6+(-3);⑦4+(-5);⑧5+(-5).
| A. | ①②③④⑤⑧ | B. | ②③⑤⑥⑦⑧ | C. | ①③④⑤⑥⑧ | D. | ①②④⑤⑦⑧ |
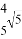 B. 斜边AB为
B. 斜边AB为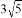
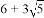
 B.
B. 

 D. 以上都不是
D. 以上都不是