题目内容
如图,在矩形ABCD中,M、N分别AD、BC的中点,P、Q分别BM、DN的中点.
(1)求证:四边形MPNQ是菱形;
(2)若AB=2,BC=4,求四边形MPNQ的面积.

(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC.
连结MN,∵M、N分别AD、BC的中点,

∴MD=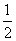 AD,BN=
AD,BN=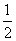 BC.
BC.
∴MD=BN,MD∥BN,∴四边形BNDM是平行四边形.
∴MB=ND.…………………………1分
∵P、Q分别BM、DN的中点,∴MP=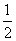 MB,NQ=
MB,NQ=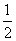 DN.
DN.
∴MP=NQ.
又∵MP∥NQ,∴四边形MPNQ是平行四边形.…………………………2分
∵ABCD为矩形,M、N分别AD、BC的中点,
∴四边形ABNM为矩形,∴MN⊥BC.
∴在Rt△MNB中 ,PN=
,PN=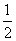 BM.∴PN=PM.………………3分
BM.∴PN=PM.………………3分
∴四边形MPNQ是菱形.…………………………4分
(2)∵AB=2,BC=4,∴MN=BN=2
∵P为MB的中点,∴PN⊥MB,PN
在Rt△MNB中,MB= …………………5分
…………………5分
∴ ,∴四边形MPNQ是边长为
,∴四边形MPNQ是边长为 的正方形.
的正方形.
∴四边形MPNQ的面积为
 ……………………………7分
……………………………7分

练习册系列答案
相关题目
某地发生特大洪灾,政府为了尽快搭建板房安置灾民,给某厂下达了生产A种板材48000㎡和B种板材24000㎡的任务.
⑴如果该厂安排210人生产这两种板材,每人每天能生产A种板材60㎡或B种板材40㎡,请问:应分别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
⑵某灾民安置点计划用该厂生产的两种板材搭建甲、乙两种规格的板房共400间,已知
建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示:
| 板房 | A种板材(m2) | B种板材(m2) | 安置人数 |
| 甲型 | 108 | 61 | 12 |
| 乙型 | 156 | 51 | 10 |
问这400间板房最多能安置多少灾民?
 中,小明对本班同学的捐款情况进行了统计,绘制成如图不完整的统计图.其中捐100元的人数占全班总人数的25%,则本次捐款的中位数是 元.
中,小明对本班同学的捐款情况进行了统计,绘制成如图不完整的统计图.其中捐100元的人数占全班总人数的25%,则本次捐款的中位数是 元.
 ·
· 的结果是 .
的结果是 . 是半圆,O为AB中点,C、D两点在
是半圆,O为AB中点,C、D两点在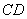 =62,则∠ABD的度数为 .
=62,则∠ABD的度数为 .
 B.
B.  C.
C.  D.
D. 
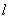 上,AB=10cm,⊙B的半径为1cm,点C在直线
上,AB=10cm,⊙B的半径为1cm,点C在直线