题目内容
18.如图①是一个直角三角形纸片,∠A=30°,BC=4cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③(1)求证:AD=BD;
(2)求折痕DE的长.

分析 (1)由折叠的性质,可求得BC′的长,然后在Rt△ABC中,∠A=30°,BC=4 cm,可求得AB的长,继而求得AC′的长,易得DC′为线段AB的垂直平分线,继而证得结论;
(2)首先在Rt△DCB中,∠DBC′=30°,求得DC′的长,然后在Rt△DC′E中,∠EDC′=30°,求得答案.
解答 解:(1)证明:由翻折可知,BC′=BC=4,
在Rt△ABC中,∠A=30°,BC=4 cm,
∴AB=2BC=8 cm
∴AC′=8-4=4 cm,
∴AC′=BC′,
又∵∠DC′B=∠C=90°,
∴DC′为线段AB的垂直平分线,
∴AD=BD;
(2)解:∴在Rt△DCB中,∠DBC′=30°,
∴DC′=$\frac{BC′}{\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$,
在Rt△DC′E中,∠EDC′=30°,
∴DE=$\frac{2}{\sqrt{3}}$DC′=$\frac{8}{3}$.
点评 此题考查了折叠的性质、含30°角的直角三角形的性质以及线段垂直平分线的性质.注意掌握折叠前后图形的对应关系是解此题的关键.

练习册系列答案
相关题目
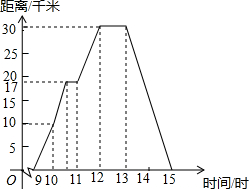 小明某天上午9时骑自行车离开家,15时回家,他描绘了离家的距离与时间的变化情况.
小明某天上午9时骑自行车离开家,15时回家,他描绘了离家的距离与时间的变化情况.
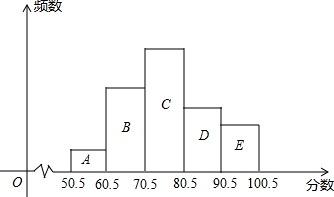 从某校参加科普知识竞赛的学生试卷中,抽取一个样本了解竞赛成绩的分布情况,将样本分成A、B、C、D、E五个组,绘制成如图所示的频数分布直方图,图中A、B、C、D、E各小组的长方形的高的比是l:4:6:3:2,且A组的频数是5,请结合直方图提供的信息,解答下列问题.
从某校参加科普知识竞赛的学生试卷中,抽取一个样本了解竞赛成绩的分布情况,将样本分成A、B、C、D、E五个组,绘制成如图所示的频数分布直方图,图中A、B、C、D、E各小组的长方形的高的比是l:4:6:3:2,且A组的频数是5,请结合直方图提供的信息,解答下列问题.