题目内容
 如图,直线AB∥CD,直线EF分别交AB于点E,交CD于点F,EG平分∠BEF交CD于点G,若∠EFC=48°,求∠EGC的度数.
如图,直线AB∥CD,直线EF分别交AB于点E,交CD于点F,EG平分∠BEF交CD于点G,若∠EFC=48°,求∠EGC的度数.考点:平行线的性质
专题:
分析:根据两直线平行,同旁内角互补求出∠BEF,再根据角平分线的定义可得∠BEG=
∠BEF,然后根据两直线平行,同旁内角互补列式计算即可得解.
| 1 |
| 2 |
解答:解:∵AB∥CD,
∴∠BEF=180°-∠EFC=180°-48°=132°,
∵EG平分∠BEF,
∴∠BEG=
∠BEF=
×132°=66°,
∵AB∥CD,
∴∠EGC=180°-∠BEG=180°-66°=114°.
∴∠BEF=180°-∠EFC=180°-48°=132°,
∵EG平分∠BEF,
∴∠BEG=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴∠EGC=180°-∠BEG=180°-66°=114°.
点评:本题考查了平行线的性质,角平分线的定义,熟记性质并准确识图是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知x=0是二次方程(m+1)x2+mx+4m2-4=0的一个解,那么m的值是( )
| A、0 | B、1 | C、-1 | D、±1 |
 如图:AD∥BC,AE平分∠BAD,CD与AE相交于M,且∠3=∠E,试说明:AB∥DC.
如图:AD∥BC,AE平分∠BAD,CD与AE相交于M,且∠3=∠E,试说明:AB∥DC.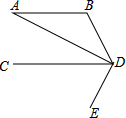 如图,已知AB∥CD,DA平分∠BDC,DE⊥AD于D,∠B=110°,求∠BDE的度数.
如图,已知AB∥CD,DA平分∠BDC,DE⊥AD于D,∠B=110°,求∠BDE的度数. 如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于F,连接AF、CE.
如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于F,连接AF、CE.
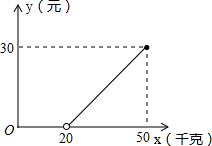 某长途汽车公司规定:乘客坐车最多可以免费携带20kg重量的行李,如果超过这个重量(但是不能超过50kg),那么需要购买行李票.假设行李票的价格y(元)与行李的重量x(kg)之间是一次函数关系,其图象如图.求:
某长途汽车公司规定:乘客坐车最多可以免费携带20kg重量的行李,如果超过这个重量(但是不能超过50kg),那么需要购买行李票.假设行李票的价格y(元)与行李的重量x(kg)之间是一次函数关系,其图象如图.求: