题目内容
15.已知锐角三角形的两边长分别3、4,则第三边长x的取值范围是( )| A. | 1<x<7 | B. | 1<x<5 | C. | $\sqrt{7}$<x<5 | D. | 1<x<$\sqrt{7}$ |
分析 分两种情况来做,当x为最大边时,只要保证x所对的角为锐角就可以了;当x不是最大边时,则4为最大边,同理只要保证4所对的角为锐角就可以了.
解答 解:分两种情况来做,当x为最大边时,由勾股定理的逆定理可知只要42+32-x2>0即可,解得4<x<5;
当x不是最大边时,则4为最大边,同理只要保证4所对的角为锐角就可以了,则有32+x2-42>0,解得$\sqrt{7}$<x≤4;
综上可知,x的取值范围为$\sqrt{7}$<x<5.
故选:C.
点评 此题考查了三角形形状的判断,涉及的知识有余弦定理,三角形的边角关系,以及一元二次不等式的解法,利用了分类讨论的数学思想.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
17.若直角三角形两边长分别是6,8,则它的斜边为( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 以上都不正确 |
20.算式[(-8)-□]÷(-2)=4中,□表示的数是( )
| A. | 1 | B. | -1 | C. | -2 | D. | 0 |
4.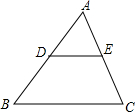 如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
 如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
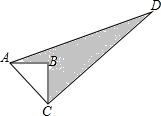 如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.
如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.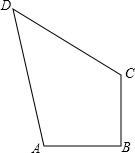 如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( ) 如图,AB与DE相交于点O,OC⊥AB,OF是∠AOE的角平分线,若∠COD=36°,则∠AOF=27°.
如图,AB与DE相交于点O,OC⊥AB,OF是∠AOE的角平分线,若∠COD=36°,则∠AOF=27°.