题目内容
一个函数具有下列性质:①它的图象经过点(-1,1);②它的图象在二、四象限内;③在每个象限内,函数值y随自变量x的增大而增大.则这个函数的解析式可以为( )
| A、y=-x+1 | ||
B、y=
| ||
| C、y=-x2 | ||
D、y=-
|
考点:反比例函数的性质,一次函数的性质,二次函数的图象
专题:
分析:先根据②可知其函数是反比例函数,再由③得出k<0,根据①可得出k的值,进而得出结论.
解答:解:∵它的图象在二、四象限内,
∴其函数是反比例函数.
∵在每个象限内,函数值y随自变量x的增大而增大,
∴k<0.
∵它的图象经过点(-1,1),
∴k=-1,
∴这个函数的解析式为y=-
.
故选D.
∴其函数是反比例函数.
∵在每个象限内,函数值y随自变量x的增大而增大,
∴k<0.
∵它的图象经过点(-1,1),
∴k=-1,
∴这个函数的解析式为y=-
| 1 |
| x |
故选D.
点评:本题考查的是反比例函数的性质,熟知反比例函数的增减性是解答此题的关键.

练习册系列答案
相关题目
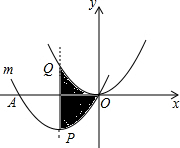 如图,把抛物线y=
如图,把抛物线y=| 1 |
| 2 |
| 1 |
| 2 |
| A、9 | ||
B、
| ||
C、
| ||
D、
|
下列四个算式中,正确的是( )
| A、a3•a2=2a6 |
| B、b3+b3=b6 |
| C、x•x4=x4 |
| D、y5+y5=2y5 |
已知两圆的半径分别为7和1,当它们内切时,圆心距为( )
| A、6 | B、7 | C、8 | D、9 |
下列说法正确的是( )
| A、-2不是单项式 | ||
| B、-a表示负数 | ||
C、
| ||
D、
|
给出四个数:-1,-
,0.5,
,其中为无理数的是( )
| 22 |
| 7 |
| 2014 |
| A、-1 | ||
B、-
| ||
| C、0.5 | ||
D、
|
方程x2=2x的解是( )
| A、x=0 | ||
| B、x=2 | ||
| C、x1=0 x2=2 | ||
D、x1=0 x2=
|
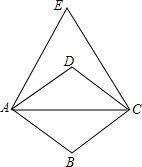 如图,四边形ABCD是菱形,以对角线AC为边向上作等边△ACE.已知∠DAB=70°,则∠EAD的大小为( )
如图,四边形ABCD是菱形,以对角线AC为边向上作等边△ACE.已知∠DAB=70°,则∠EAD的大小为( )| A、25° | B、35° |
| C、45° | D、55° |
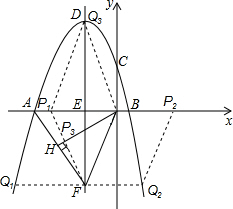 如图,抛物线y=ax2+bx+c与坐标轴分别交于A(-3,0),B(1,0),C(0,3),D是抛物线顶点,E是对称轴与x轴的交点
如图,抛物线y=ax2+bx+c与坐标轴分别交于A(-3,0),B(1,0),C(0,3),D是抛物线顶点,E是对称轴与x轴的交点