题目内容
7.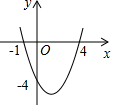 已知抛物线y=x2-3kx+2k+4
已知抛物线y=x2-3kx+2k+4(1)k为何值时,抛物线关于y轴对称;
(2)k为何值时,抛物线经过原点.
分析 (1)抛物线关于y轴对称,则x1+x2=0,解方程即可;
(2)根据抛物线经过原点得到方程2k+4=0,解方程即可.
解答 解:(1)设二次函数图象与x轴两交点坐标分别为(x1,0)(x2,0),
∵抛物线关于y轴对称,
∴x1+x2=0,
即3k=0,
解得:k=0,
∴当k=0时,抛物线关于y轴对称;
(2)∵抛物线经过原点,
∴2k+4=0,
解得:k=-2,
∴k为-2时,抛物线经过原点.
点评 本题主要考查了二次函数与一元二次方程的关系,熟悉一元二次方程根与系数的关系与二次函数与x轴交点位置的对应关系是解决问题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
2.-2的倒数是( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
12.某房地产开发公司计划建A、B两种户型的住房共80套,A种户型每套成本和售价分别为90万元和102万元,B种户型每套成本和售价分别为60万元和70万元.设计划建A户型x套,所建户型全部售出后获得的总利润为W万元.
【思考】
(1)根据所给条件,完成下表:
(2)求W与x之间的函数解析式;
【探究】
(3)该公司所建房资金不少于5700万元,且所筹资金全部用于建房,若A户型不超过32套,则该公司有哪几种建房方案?
(4)在(3)的前提下,根据国家房地产政策,公司计划每套A户型住房的售价降低a万元(0<a≤3),B户型住房的售价不变,且预计所建的两种住房全部售出,求该公司获得最大利润的方案.
【决策】
为了适应市场需要,该公司在总套数不变的情况下,改建若干套C户型,现已知C户型每套成本110万元,售价118万元.若该公司所筹资金为6300万元且刚好用完,则当x=45套时,该公司所建房售出后获得的总利润最大.
【思考】
(1)根据所给条件,完成下表:
| A户型 | B户型 | |
| 套数 | x | 80-x |
| 利润(万元) | 12x | 10(80-x) |
【探究】
(3)该公司所建房资金不少于5700万元,且所筹资金全部用于建房,若A户型不超过32套,则该公司有哪几种建房方案?
(4)在(3)的前提下,根据国家房地产政策,公司计划每套A户型住房的售价降低a万元(0<a≤3),B户型住房的售价不变,且预计所建的两种住房全部售出,求该公司获得最大利润的方案.
【决策】
为了适应市场需要,该公司在总套数不变的情况下,改建若干套C户型,现已知C户型每套成本110万元,售价118万元.若该公司所筹资金为6300万元且刚好用完,则当x=45套时,该公司所建房售出后获得的总利润最大.
19.若点A(a,-2)、B(4,b)在正比例函数y=kx的图象上,则下列等式一定成立的是( )
| A. | a-b=6 | B. | a+b=-10 | C. | a•b=-8 | D. | $\frac{a}{b}$=-2 |
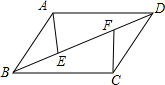 如图所示,已知点E,F在?ABCD的对角线BD上,且BF=DE,求证:AE=CF.
如图所示,已知点E,F在?ABCD的对角线BD上,且BF=DE,求证:AE=CF.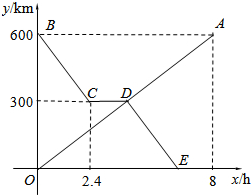 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发3h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发3h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.