题目内容
现有一列数a1，a2，a3，…，a2008，a2009，a2010，其中a2=-1，a31=-7，a2010=9，且满足任意相邻三个数的和为相等的常数，则a1+a2+a3+…+a98+a99+a100的值为（ ）
| A、0 | B、40 | C、32 | D、26 |
考点：有理数无理数的概念与运算
专题：规律型
分析：由已知可推出a1=a4=a7=…=a31=…=a2008=-7，a2=a5=a8=…=a2009=-1，a3=a6=a9=…=a2010=9，由此可求a1+a2+a3+…+a98+a99+a100的值．
解答：解：∵a1+a2+a3=a2+a3+a4，
∴a1=a4，
同理可得
a1=a4=a7=…=a100=a31=-7，
a2=a5=a8=…=a98=-1，
a3=a6=a9=…=a99=a2010=9，
由各数出现的规律可知，从a1开始到a100的数列中，
-7出现了34次，-1出现了33次，9出现了33次，
则a1+a2+a3+…+a98+a99+a100
=（-7）×34+（-1）×33+9×33
=26．
故选D．
∴a1=a4，
同理可得
a1=a4=a7=…=a100=a31=-7，
a2=a5=a8=…=a98=-1，
a3=a6=a9=…=a99=a2010=9，
由各数出现的规律可知，从a1开始到a100的数列中，
-7出现了34次，-1出现了33次，9出现了33次，
则a1+a2+a3+…+a98+a99+a100
=（-7）×34+（-1）×33+9×33
=26．
故选D．
点评：本题考查了有理数无理数的概念与运算．关键是根据题目所给条件，得出各数重复的规律．
练习册系列答案
相关题目
方程x（x-1）=x的解为（ ）
| A、x=2 |
| B、x=1 |
| C、x=0或x=1 |
| D、x=0或x=2 |
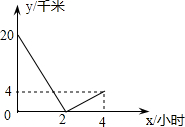甲、乙二人从A、B两地同时出发相向而行，相遇后，甲立即返回，先于乙回到A地，两人相距的路程y（千米）与行驶时间x（小时）之间的函数关系如图所示，则乙从B地到A地需时间
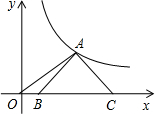如图，等腰Rt△ABC的斜边BC在x轴上，顶点A在反比例函数 
小红制作了一个对面图案均相同的正方体礼品盒，（如图所示），则这们礼品盒的平面展开图是（ ）
