题目内容
9.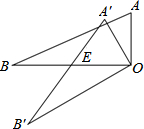 如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△AOB处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为$\frac{9\sqrt{5}}{5}$.
如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△AOB处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为$\frac{9\sqrt{5}}{5}$.
分析 利用勾股定理列式求出AB,根据旋转的性质可得AO=A′O,A′B′=AB,再求出OE,从而得到OE=A′O,过点O作OF⊥A′B′于F,利用三角形的面积求出OF,利用勾股定理列式求出EF,再根据等腰三角形三线合一的性质可得A′E=2EF,然后根据B′E=A′B′-A′E代入数据计算即可得解.
解答 解:∵∠AOB=90°,AO=3,BO=6,
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
∵△AOB绕顶点O逆时针旋转到△A′OB′处,
∴AO=A′O=3,A′B′=AB=3$\sqrt{5}$,
∵点E为BO的中点,
∴OE=$\frac{1}{2}$BO=$\frac{1}{2}$×6=3,
∴OE=A′O, 过点O作OF⊥A′B′于F,
过点O作OF⊥A′B′于F,
S△A′OB′=$\frac{1}{2}$×3$\sqrt{5}$•OF=$\frac{1}{2}$×3×6,
解得OF=$\frac{6\sqrt{5}}{5}$,
在Rt△EOF中,EF=$\sqrt{O{E}^{2}-O{F}^{2}}$=$\sqrt{{3}^{2}-(\frac{6\sqrt{5}}{5})^{2}}$=$\frac{3\sqrt{5}}{5}$,
∵OE=A′O,OF⊥A′B′,
∴A′E=2EF=2×$\frac{3\sqrt{5}}{5}$=$\frac{6\sqrt{5}}{5}$(等腰三角形三线合一),
∴B′E=A′B′-A′E=3$\sqrt{5}$-$\frac{6\sqrt{5}}{5}$=$\frac{9\sqrt{5}}{5}$.
故答案为:$\frac{9\sqrt{5}}{5}$.
点评 本题考查了旋转的性质,勾股定理的应用,等腰三角形三线合一的性质,以及三角形面积,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.

 阶梯计算系列答案
阶梯计算系列答案| A. | 当k≠0时,方程总有两个不相等的实数解 | |
| B. | 当k=-1时,方程有两个相等的实数解 | |
| C. | 当k=1时,方程有一个实数解 | |
| D. | 当k=0时,方程无解 |
| A. | ((13-x)=20 | B. | x($\frac{13-x}{2}$)=20 | C. | x(13-$\frac{1}{2}$x)=20 | D. | x($\frac{13-2x}{2}$)=20 |
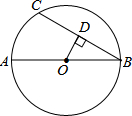 如图,AB为圆O的直径,BC为圆O的一弦,自O点作BC的垂线,且交BC于D点.若AB=16,BC=12,则△OBD的面积为何?( )
如图,AB为圆O的直径,BC为圆O的一弦,自O点作BC的垂线,且交BC于D点.若AB=16,BC=12,则△OBD的面积为何?( )| A. | 6$\sqrt{7}$ | B. | 12$\sqrt{7}$ | C. | 15 | D. | 30 |
| 水果名称 | 草莓 | 苹果 | 荔枝 |
| 每箱价格(元) | 60 | 40 | 90 |
(2)李心有甲、乙两店铺,每个店铺在同一时间段内都能售出草莓、苹果两种水果合计30箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为30元和40元,乙店铺获毛利润分别为27元和36元.现在,李心购进草莓35箱,苹果25箱.怎样分配给每个店铺各30箱水果,使得在保证乙店铺获毛利润不少于950元的前提下,李心获取的总毛利润W最大?最大的总毛利润是多少元?
(3)李心购买上述三种水果共20箱,恰好花费1030元,则他购买了3或1箱荔枝.(直接写出答案)
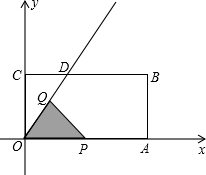 如图,已知矩形ABCD中,OA=8,AB=1,直线y=$\frac{4}{3}$x交BC于D,动点P、Q同时从D出发,点P沿折线OA-AB-BD以每秒3个单位的速度运动到D停止,点Q沿射线OD以每秒1个单位的速度运动,当点P停止时,点Q也停止运动.△OPQ与梯形OABD重叠部分的面积为S,运动时间为t.
如图,已知矩形ABCD中,OA=8,AB=1,直线y=$\frac{4}{3}$x交BC于D,动点P、Q同时从D出发,点P沿折线OA-AB-BD以每秒3个单位的速度运动到D停止,点Q沿射线OD以每秒1个单位的速度运动,当点P停止时,点Q也停止运动.△OPQ与梯形OABD重叠部分的面积为S,运动时间为t.