题目内容
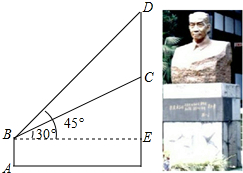 如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:
如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:几何图形问题
分析:首先分析图形:根据题意构造两个直角三角形△DEB、△CEB,再利用其公共边BE求得DE、CE,再根据CD=DE-CE计算即可求出答案.
解答:解:在Rt△DEB中,DE=BE•tan45°=2.7米,
在Rt△CEB中,CE=BE•tan30°=0.9
米,
则CD=DE-CE=2.7-0.9
≈1.2米.
故塑像CD的高度大约为1.2米.
在Rt△CEB中,CE=BE•tan30°=0.9
| 3 |
则CD=DE-CE=2.7-0.9
| 3 |
故塑像CD的高度大约为1.2米.
点评:本题考查解直角三角形的知识.要先将实际问题抽象成数学模型.分别在两个不同的三角形中,借助三角函数的知识,研究角和边的关系.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
方程
-
=0解是( )
| 3 |
| x |
| 7 |
| x+1 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
| D、x=-1 |
 如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最小值是
如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最小值是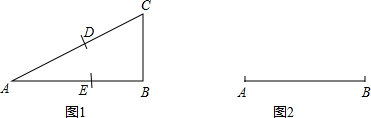
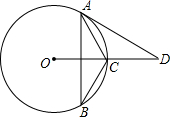 如图,⊙O中,点C为
如图,⊙O中,点C为
 如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.